Examining Asymmetric Encryption and PKI
![]() Asymmetric encryption algorithms accomplish two primary objectives: confidentiality and authentication. Asymmetric algorithms are slower than symmetric algorithms because they use more complex mathematics. Because asymmetric algorithms are slower, they are usually used as key exchange protocols. The sections that follow cover the principles behind asymmetric encryption and provide examples of major asymmetric encryption algorithms, including Rivest, Shamir, and Adleman (RSA), Diffie-Hellman (DH), and Public Key Infrastructure (PKI).
Asymmetric encryption algorithms accomplish two primary objectives: confidentiality and authentication. Asymmetric algorithms are slower than symmetric algorithms because they use more complex mathematics. Because asymmetric algorithms are slower, they are usually used as key exchange protocols. The sections that follow cover the principles behind asymmetric encryption and provide examples of major asymmetric encryption algorithms, including Rivest, Shamir, and Adleman (RSA), Diffie-Hellman (DH), and Public Key Infrastructure (PKI).
 Asymmetric Encryption Overview
Asymmetric Encryption Overview
![]() To provide the two main objectives of confidentiality and authentication, asymmetric algorithms are based on considerably more complex mathematical formulas than symmetric algorithms. As a result, computation takes more time for asymmetric algorithms. Despite this slower computation trait, asymmetric algorithms are often used as key exchange protocols for symmetric algorithms, which have no inherent key exchange technology.
To provide the two main objectives of confidentiality and authentication, asymmetric algorithms are based on considerably more complex mathematical formulas than symmetric algorithms. As a result, computation takes more time for asymmetric algorithms. Despite this slower computation trait, asymmetric algorithms are often used as key exchange protocols for symmetric algorithms, which have no inherent key exchange technology.
![]() Also known as public key encryption, asymmetric algorithms have two keys: a public key and a private key. Both keys are capable of the encryption process. However, the complimentary matched key is required for decryption. For example, if a public key encrypts the data, the matching private key decrypts the data. The opposite is also true. If a private key encrypts the data, the corresponding public key decrypts the data.
Also known as public key encryption, asymmetric algorithms have two keys: a public key and a private key. Both keys are capable of the encryption process. However, the complimentary matched key is required for decryption. For example, if a public key encrypts the data, the matching private key decrypts the data. The opposite is also true. If a private key encrypts the data, the corresponding public key decrypts the data.
![]() Examples of public-key encryption algorithms are RSA, DSA, DH, ElGamal, and ECC. The mathematics differ with each algorithm, but they all share one trait: The mathematics can be complicated.
Examples of public-key encryption algorithms are RSA, DSA, DH, ElGamal, and ECC. The mathematics differ with each algorithm, but they all share one trait: The mathematics can be complicated.
![]() Figure 4-11, shown earlier, illustrates the mechanics of asymmetric encryption.
Figure 4-11, shown earlier, illustrates the mechanics of asymmetric encryption.
![]() Asymmetric algorithms are designed in such a way that the key that is used for encryption is different from the key that is used for decryption. The decryption key cannot, in any reasonable amount of time, be calculated from the encryption key, and vice versa. The usual key length for asymmetric algorithms ranges from 512 to 4096 bits. Asymmetric algorithm key lengths cannot be directly compared to symmetric algorithm key lengths because the two algorithm families differ greatly in their underlying design.
Asymmetric algorithms are designed in such a way that the key that is used for encryption is different from the key that is used for decryption. The decryption key cannot, in any reasonable amount of time, be calculated from the encryption key, and vice versa. The usual key length for asymmetric algorithms ranges from 512 to 4096 bits. Asymmetric algorithm key lengths cannot be directly compared to symmetric algorithm key lengths because the two algorithm families differ greatly in their underlying design.
![]() To illustrate this point, it is generally thought that an encryption key of RSA that is 2048 bits is roughly equivalent to a 128-bit key of RC4 in terms of resistance against brute-force attacks.
To illustrate this point, it is generally thought that an encryption key of RSA that is 2048 bits is roughly equivalent to a 128-bit key of RC4 in terms of resistance against brute-force attacks.
![]() The best-known asymmetric cryptographic algorithms are RSA, ElGamal, and elliptic curve algorithms.
The best-known asymmetric cryptographic algorithms are RSA, ElGamal, and elliptic curve algorithms.
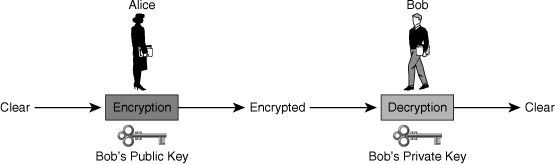
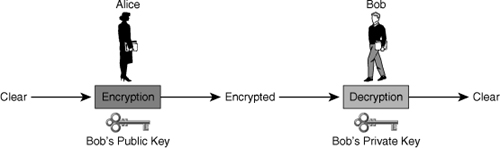
![]() The confidentiality objective of asymmetric algorithms is achieved when the encryption process is started with the public key. When the public key is used to encrypt the data, the private key must be used to decrypt the data. Only one host has the private key; therefore, confidentiality is achieved.
The confidentiality objective of asymmetric algorithms is achieved when the encryption process is started with the public key. When the public key is used to encrypt the data, the private key must be used to decrypt the data. Only one host has the private key; therefore, confidentiality is achieved.
| Caution |
|
![]() In Figure 4-22, Alice and Bob exchange data with the goal of confidentiality. They follow these steps:
In Figure 4-22, Alice and Bob exchange data with the goal of confidentiality. They follow these steps:
|
|
|
|
|
|
|
|
|
|
|
|
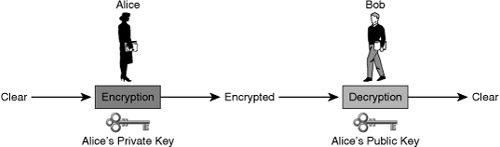
![]() The authentication objective of asymmetric algorithms is achieved when the encryption process is started with the private key. When the private key is used to encrypt the data, the public key must be used to decrypt the data. Because only one host has the private key, only that host could have encrypted the message, therefore providing authentication of the sender.
The authentication objective of asymmetric algorithms is achieved when the encryption process is started with the private key. When the private key is used to encrypt the data, the public key must be used to decrypt the data. Because only one host has the private key, only that host could have encrypted the message, therefore providing authentication of the sender.
| Key Topic |
|
![]() In addition, no attempt is typically made to preserve the secrecy of the public key, so any number of hosts can decrypt the message. When a host successfully decrypts a message using a public key, it is trusted that the private key encrypted the message, which verifies who the sender is; this is a form of authentication.
In addition, no attempt is typically made to preserve the secrecy of the public key, so any number of hosts can decrypt the message. When a host successfully decrypts a message using a public key, it is trusted that the private key encrypted the message, which verifies who the sender is; this is a form of authentication.
![]() In Figure 4-23, Alice and Bob exchange data with the goal of authentication. They follow these steps:
In Figure 4-23, Alice and Bob exchange data with the goal of authentication. They follow these steps:
|
|
|
|
|
|
|
|
|
|
|
|
 RSA: Features and Functions
RSA: Features and Functions
![]() RSA is one of the most common asymmetric algorithms. Ron Rivest, (discussed earlier in this chapter), Adi Shamir, and Len Adleman invented the patented public-key RSA algorithm in 1977. The patent expired in September 2000, and the algorithm is now in the public domain. Of all the public-key algorithms that were proposed over the years, RSA is by far the easiest to understand and implement.
RSA is one of the most common asymmetric algorithms. Ron Rivest, (discussed earlier in this chapter), Adi Shamir, and Len Adleman invented the patented public-key RSA algorithm in 1977. The patent expired in September 2000, and the algorithm is now in the public domain. Of all the public-key algorithms that were proposed over the years, RSA is by far the easiest to understand and implement.
![]() The RSA algorithm is very flexible because it has a variable key length that allows speed to be traded for the security of the algorithm if necessary.
The RSA algorithm is very flexible because it has a variable key length that allows speed to be traded for the security of the algorithm if necessary.
![]() The RSA keys are usually 512 to 2048 bits long. RSA has withstood years of extensive cryptanalysis, and although the security of RSA has been neither proved nor disproved, it does suggest a confidence level in the algorithm. The security of RSA is based on the difficulty of factoring very large numbers, which is breaking large numbers into multiplicative factors. If an easy method of factoring these large numbers were discovered, the effectiveness of RSA would be destroyed.
The RSA keys are usually 512 to 2048 bits long. RSA has withstood years of extensive cryptanalysis, and although the security of RSA has been neither proved nor disproved, it does suggest a confidence level in the algorithm. The security of RSA is based on the difficulty of factoring very large numbers, which is breaking large numbers into multiplicative factors. If an easy method of factoring these large numbers were discovered, the effectiveness of RSA would be destroyed.
![]() The RSA algorithm is based on the fact that each entity has two keys: a public key and a private key. The public key can be published and given away, but the private key must be kept very secret. It is not possible to determine, using any computationally feasible algorithm, the private key from the public key and vice versa. What one of the keys encrypts, the other key decrypts, and vice versa.
The RSA algorithm is based on the fact that each entity has two keys: a public key and a private key. The public key can be published and given away, but the private key must be kept very secret. It is not possible to determine, using any computationally feasible algorithm, the private key from the public key and vice versa. What one of the keys encrypts, the other key decrypts, and vice versa.
![]() RSA keys are long term and are usually changed or renewed after some months or even years.
RSA keys are long term and are usually changed or renewed after some months or even years.
| Note |
|
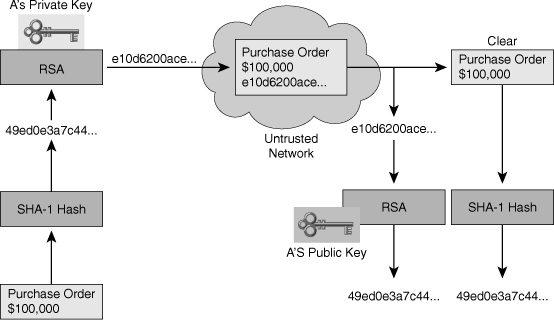
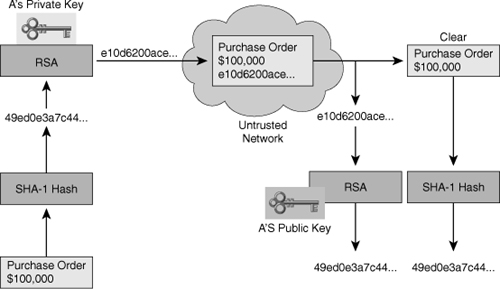
![]() The current signing procedures of digital signatures are not simply implemented by public-key operations. In fact, a modern digital signature is based on a hash function and a public-key algorithm. Figure 4-24 illustrates this procedure.
The current signing procedures of digital signatures are not simply implemented by public-key operations. In fact, a modern digital signature is based on a hash function and a public-key algorithm. Figure 4-24 illustrates this procedure.
![]() The signature process is as follows:
The signature process is as follows:
|
|
|
|
|
|
|
|
|
![]() The verification process works as follows:
The verification process works as follows:
![]() This example shown using Figure 4-24 illustrates how the authenticity and integrity of the message is ensured, even though the actual text is public. Both encryption and digital signatures are required to ensure that the message is private and has not changed.
This example shown using Figure 4-24 illustrates how the authenticity and integrity of the message is ensured, even though the actual text is public. Both encryption and digital signatures are required to ensure that the message is private and has not changed.
| Note |
|
![]() RSA is about 100 times slower than DES in hardware, and about 1000 times slower than DES in software. This performance problem is the main reason that RSA is typically used only to protect small amounts of data. RSA is mainly used for two services:
RSA is about 100 times slower than DES in hardware, and about 1000 times slower than DES in software. This performance problem is the main reason that RSA is typically used only to protect small amounts of data. RSA is mainly used for two services:
-
 To ensure confidentiality of data by performing encryption
To ensure confidentiality of data by performing encryption -
 To perform authentication of data, nonrepudiation of data, or both by generating digital signatures
To perform authentication of data, nonrepudiation of data, or both by generating digital signatures
| Note |
|
 DH: Features and Functions
DH: Features and Functions
![]() The Diffie-Hellman (DH) algorithm is the basis of most modern automatic key exchange methods. The Internet Key Exchange (IKE) protocol in IPsec VPNs uses DH algorithms extensively to provide a reliable and trusted method for key exchange over untrusted channels.
The Diffie-Hellman (DH) algorithm is the basis of most modern automatic key exchange methods. The Internet Key Exchange (IKE) protocol in IPsec VPNs uses DH algorithms extensively to provide a reliable and trusted method for key exchange over untrusted channels.
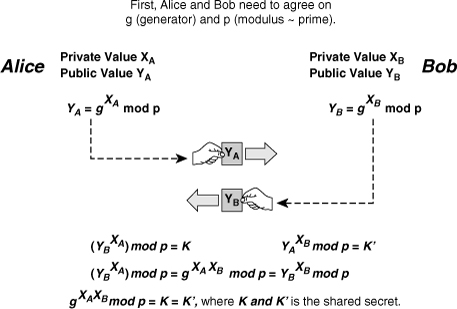
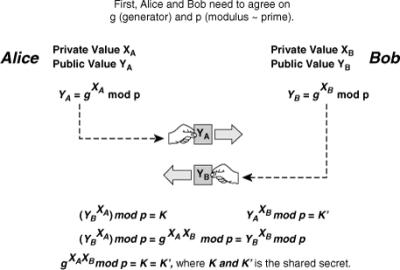
![]() Whitfield Diffie and Martin Hellman invented the DH algorithm in 1976. Its security stems from the difficulty of calculating the discrete logarithms of very large numbers. The DH algorithm, shown in Figure 4-25, provides secure key exchange over unsecure channels and is frequently used in modern key management to provide keying material for other symmetric algorithms, such as DES, 3DES, and AES.
Whitfield Diffie and Martin Hellman invented the DH algorithm in 1976. Its security stems from the difficulty of calculating the discrete logarithms of very large numbers. The DH algorithm, shown in Figure 4-25, provides secure key exchange over unsecure channels and is frequently used in modern key management to provide keying material for other symmetric algorithms, such as DES, 3DES, and AES.
![]() To start a DH exchange, the two parties must agree on two nonsecret numbers. The first number is g, the generator, and the second number is p, the modulus. These numbers can be made public and are usually chosen from a table of known values. g is usually a very small number, such as 2, 3, and 4, and p is a very large prime number. Next, every party generates its own secret value. Then, based on g, p, and the secret value of each party, each party calculates its public value. The public value is computed according to the following formula:
To start a DH exchange, the two parties must agree on two nonsecret numbers. The first number is g, the generator, and the second number is p, the modulus. These numbers can be made public and are usually chosen from a table of known values. g is usually a very small number, such as 2, 3, and 4, and p is a very large prime number. Next, every party generates its own secret value. Then, based on g, p, and the secret value of each party, each party calculates its public value. The public value is computed according to the following formula:
|
|
![]() In this formula x is the secret value of the entity, and Y is the public value of the entity.
In this formula x is the secret value of the entity, and Y is the public value of the entity.
![]() After computing the public values, the two parties exchange their public values. Each party then exponentiates the received public value with its secret value to compute a common shared-secret value, represented by K and K’ in Figure 4-25. When the algorithm completes, both parties have the same shared secret, which they have computed from their secret value and the public value of the other party.
After computing the public values, the two parties exchange their public values. Each party then exponentiates the received public value with its secret value to compute a common shared-secret value, represented by K and K’ in Figure 4-25. When the algorithm completes, both parties have the same shared secret, which they have computed from their secret value and the public value of the other party.
![]() No one listening on the channel can compute the secret value, because only g, p, YA, and YB are known; at least one secret value is needed to calculate the shared secret. Unless attackers can compute the discrete algorithm of the above equation to recover XA or XB, they cannot obtain the shared secret.
No one listening on the channel can compute the secret value, because only g, p, YA, and YB are known; at least one secret value is needed to calculate the shared secret. Unless attackers can compute the discrete algorithm of the above equation to recover XA or XB, they cannot obtain the shared secret.
![]() The following steps describe a DH exchange:
The following steps describe a DH exchange:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() Alice and Bob now have a shared secret (k = k’) and even if someone has listened on the untrusted channel, there is no way the listener could compute the secret from the captured information, assuming that computing a discrete logarithm of YA or YB is practically unfeasible.
Alice and Bob now have a shared secret (k = k’) and even if someone has listened on the untrusted channel, there is no way the listener could compute the secret from the captured information, assuming that computing a discrete logarithm of YA or YB is practically unfeasible.
| Note |
|
 PKI Definitions and Algorithms
PKI Definitions and Algorithms
![]() With trusted third-party protocols, all individuals agree to accept the word of a neutral third party. In this way, the parties that need to validate each other rely on the in-depth authentication of an agreed upon third party, instead of performing their own authentication. Presumably, the third party does an in-depth investigation before the issuance of credentials, and, after this in-depth investigation, the third party issues credentials that are difficult to forge. From that point forward, all individuals who trust the third party simply accept the credentials that the third party issues.
With trusted third-party protocols, all individuals agree to accept the word of a neutral third party. In this way, the parties that need to validate each other rely on the in-depth authentication of an agreed upon third party, instead of performing their own authentication. Presumably, the third party does an in-depth investigation before the issuance of credentials, and, after this in-depth investigation, the third party issues credentials that are difficult to forge. From that point forward, all individuals who trust the third party simply accept the credentials that the third party issues.
![]() In large organizations, it is impractical for all parties to continually exchange identification documents. For example, Cisco goes to reasonable measures to identify employees and contractors, and then issues an ID badge. This badge is relatively difficult to forge; measures are in place to protect the integrity of the badge and the badge issuance. Because of these measures, all Cisco personnel accept this badge as authoritative as to the identity of any individual.
In large organizations, it is impractical for all parties to continually exchange identification documents. For example, Cisco goes to reasonable measures to identify employees and contractors, and then issues an ID badge. This badge is relatively difficult to forge; measures are in place to protect the integrity of the badge and the badge issuance. Because of these measures, all Cisco personnel accept this badge as authoritative as to the identity of any individual.
![]() If this method did not exist and 10 individuals needed to validate each other, 90 validations would need to be performed before everyone would have validated everyone else. The formula is n(n − 1), so 10(10 − 1) gives you the 90 validations. Adding a single individual to the group would require an additional 20 validations because each one of the original 10 individuals would need to authenticate the new individual, and the new individual would need to authenticate the original 10. This method does not scale well.
If this method did not exist and 10 individuals needed to validate each other, 90 validations would need to be performed before everyone would have validated everyone else. The formula is n(n − 1), so 10(10 − 1) gives you the 90 validations. Adding a single individual to the group would require an additional 20 validations because each one of the original 10 individuals would need to authenticate the new individual, and the new individual would need to authenticate the original 10. This method does not scale well.
| Note |
|
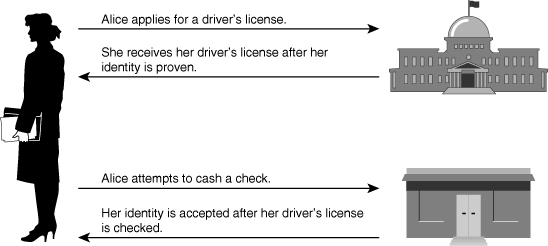
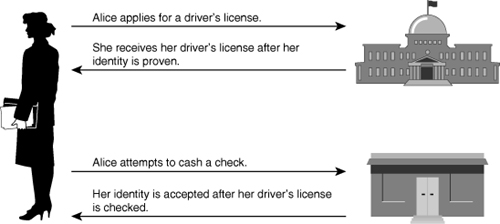
![]() In Figure 4-26, Alice applies for a driver’s license. In this process, she will submit evidence of her identity and her qualifications to drive. Her application is approved and a license is issued.
In Figure 4-26, Alice applies for a driver’s license. In this process, she will submit evidence of her identity and her qualifications to drive. Her application is approved and a license is issued.
![]() Later, Alice needs to cash a check at the bank. Upon presenting the check to the bank teller, the bank teller asks her for ID. The bank, because it trusts the government agency that issued the driver’s license, verifies her identity, and cashes her check.
Later, Alice needs to cash a check at the bank. Upon presenting the check to the bank teller, the bank teller asks her for ID. The bank, because it trusts the government agency that issued the driver’s license, verifies her identity, and cashes her check.
| Note |
|
![]() A PKI provides a framework upon which you can base security services, such as encryption, authentication, and nonrepudiation. A PKI allows for very scalable solutions, and is becoming an extremely important authentication solution for VPNs. A PKI uses specific terminology to name its components.
A PKI provides a framework upon which you can base security services, such as encryption, authentication, and nonrepudiation. A PKI allows for very scalable solutions, and is becoming an extremely important authentication solution for VPNs. A PKI uses specific terminology to name its components.
PKI Terminology
![]() When these concepts are applied in practice, it is important to understand the supporting framework. A PKI is the service framework that is needed to support large-scale, public-key-based technologies. PKI is a set of technical, organizational, and legal components that are needed to establish a system that enables large-scale use of public-key cryptography to provide authenticity, confidentiality, integrity, and nonrepudiation services.
When these concepts are applied in practice, it is important to understand the supporting framework. A PKI is the service framework that is needed to support large-scale, public-key-based technologies. PKI is a set of technical, organizational, and legal components that are needed to establish a system that enables large-scale use of public-key cryptography to provide authenticity, confidentiality, integrity, and nonrepudiation services.
![]() Two very important terms must be defined when talking about a PKI:
Two very important terms must be defined when talking about a PKI:
-
 Certificate authority (CA): The trusted third party that signs the public keys of entities in a PKI-based system
Certificate authority (CA): The trusted third party that signs the public keys of entities in a PKI-based system -
 Certificate: A document that in essence binds together the name of the entity and its public key and that has been signed by the CA
Certificate: A document that in essence binds together the name of the entity and its public key and that has been signed by the CA
| Note |
|
| Key Topic |
|
PKI Components
![]() PKI is more than just a CA and its users. And implementing the enabling technology and building a large PKI involves a huge amount of organizational and legal work. There are five main areas of a PKI:
PKI is more than just a CA and its users. And implementing the enabling technology and building a large PKI involves a huge amount of organizational and legal work. There are five main areas of a PKI:
-
 CAs for key management
CAs for key management -
 PKI users, such as people, devices, servers, and so on
PKI users, such as people, devices, servers, and so on -
 Storage and protocols
Storage and protocols -
 Supporting organizational framework, known as practices and user authentication using local registration authorities (LRA)
Supporting organizational framework, known as practices and user authentication using local registration authorities (LRA) -
 Supporting legal framework
Supporting legal framework
![]() Many vendors offer CA servers as a managed service or as an end-user product:
Many vendors offer CA servers as a managed service or as an end-user product:
Certificate Classes
![]() CAs, especially outsourced ones, can issue certificates of a number of classes, which determine how trusted a certificate is. A single outsourcing vendor (for example, VeriSign) might run a single CA, issuing certificates of different classes, and its customers will use the CA they need depending on the desired level of trust.
CAs, especially outsourced ones, can issue certificates of a number of classes, which determine how trusted a certificate is. A single outsourcing vendor (for example, VeriSign) might run a single CA, issuing certificates of different classes, and its customers will use the CA they need depending on the desired level of trust.
![]() A certificate class is usually a number; the higher the number, the more trusted the certificate is considered. The trust in the certificate is usually determined by how rigorous the procedure was that verified the identity of the holder when the certificate was issued. For example, a class 0 certificate might be issued without any checks, such as for testing purposes. A class 1 certificate might require an email reply from the holder to confirm his wish to enroll. This confirmation is a weak authentication of the holder. For a class 3 or 4 certificate, the future holder must prove his identity and authenticate their public key by showing up in person, with at least two official ID documents.
A certificate class is usually a number; the higher the number, the more trusted the certificate is considered. The trust in the certificate is usually determined by how rigorous the procedure was that verified the identity of the holder when the certificate was issued. For example, a class 0 certificate might be issued without any checks, such as for testing purposes. A class 1 certificate might require an email reply from the holder to confirm his wish to enroll. This confirmation is a weak authentication of the holder. For a class 3 or 4 certificate, the future holder must prove his identity and authenticate their public key by showing up in person, with at least two official ID documents.
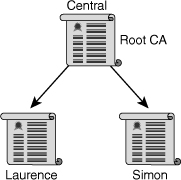
![]() PKIs also form different topologies of trust. In the simple model, a single CA, which is also known as the root CA, issues all the certificates to the end users, as shown in Figure 4-27. The benefit in such a setup is simplicity, but there are several pitfalls:
PKIs also form different topologies of trust. In the simple model, a single CA, which is also known as the root CA, issues all the certificates to the end users, as shown in Figure 4-27. The benefit in such a setup is simplicity, but there are several pitfalls:
-
 It is difficult to scale this topology to a large environment.
It is difficult to scale this topology to a large environment. -
 This topology needs a strictly centralized administration.
This topology needs a strictly centralized administration. -
 There is a critical vulnerability in using a single-signing private key; if this key is stolen, the whole PKI falls apart because the CA can no longer be trusted as a unique signer.
There is a critical vulnerability in using a single-signing private key; if this key is stolen, the whole PKI falls apart because the CA can no longer be trusted as a unique signer.
![]() Because of its simplicity, VPNs that are managed by a single organization often use this topology.
Because of its simplicity, VPNs that are managed by a single organization often use this topology.
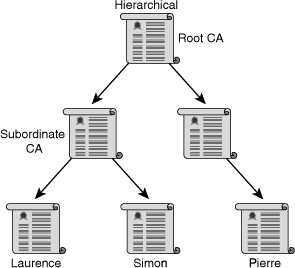
![]() Going beyond the single-root CA, topologies that are more complex can be devised that involve multiple CAs within the same organization. One such topology is the hierarchical CA system, shown in Figure 4-28. With the hierarchical topology, CAs can issue certificates to end users and to subordinate CAs, which in turn issue their certificates to end users, other CAs, or both. Therefore, a tree of CAs and end users is built in which every CA can issue certificates to lower-level CAs and end users.
Going beyond the single-root CA, topologies that are more complex can be devised that involve multiple CAs within the same organization. One such topology is the hierarchical CA system, shown in Figure 4-28. With the hierarchical topology, CAs can issue certificates to end users and to subordinate CAs, which in turn issue their certificates to end users, other CAs, or both. Therefore, a tree of CAs and end users is built in which every CA can issue certificates to lower-level CAs and end users.
![]() The main benefits of a hierarchical PKI topology are increased scalability and manageability; trust decisions can now be hierarchically distributed to smaller branches. This distribution works well in most large organizations. For example, a large company may have a root CA that issues certificates to level-2 CAs. These level-2 CAs issue the certificates to the end users. Because the root-signing key is seldom used after the subordinate CA certificates are issued, it is less exposed and therefore much more trusted. Also, if a subordinate CA has its private key stolen, only a branch of the PKI is rendered untrusted. All other users can consider this by no longer trusting that particular CA.
The main benefits of a hierarchical PKI topology are increased scalability and manageability; trust decisions can now be hierarchically distributed to smaller branches. This distribution works well in most large organizations. For example, a large company may have a root CA that issues certificates to level-2 CAs. These level-2 CAs issue the certificates to the end users. Because the root-signing key is seldom used after the subordinate CA certificates are issued, it is less exposed and therefore much more trusted. Also, if a subordinate CA has its private key stolen, only a branch of the PKI is rendered untrusted. All other users can consider this by no longer trusting that particular CA.
![]() One issue with hierarchical PKI topologies lies in finding the certification path for a certificate (in other words, determining the chain of the signing process). The more CAs involved in establishing the trust between the root CA and the end user, the more difficult the task.
One issue with hierarchical PKI topologies lies in finding the certification path for a certificate (in other words, determining the chain of the signing process). The more CAs involved in establishing the trust between the root CA and the end user, the more difficult the task.
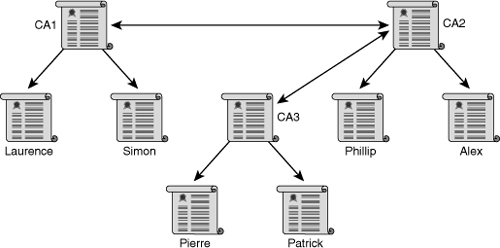
![]() Another approach to hierarchical PKIs is called cross-certifying, as shown in Figure 4-29. In this scenario, multiple flat single-root CAs establish trust relationships horizontally, by cross-certifying their own CA certificates.
Another approach to hierarchical PKIs is called cross-certifying, as shown in Figure 4-29. In this scenario, multiple flat single-root CAs establish trust relationships horizontally, by cross-certifying their own CA certificates.
![]() Some PKIs might offer the possibility or even require the use of two key pairs per entity:
Some PKIs might offer the possibility or even require the use of two key pairs per entity:
-
 One public and private key pair is intended only for encryption operations. The public key encrypts, and the private key decrypts.
One public and private key pair is intended only for encryption operations. The public key encrypts, and the private key decrypts. -
 The other public and private key pair is intended only for signing operations. The private key signs, and the public key verifies the signature.
The other public and private key pair is intended only for signing operations. The private key signs, and the public key verifies the signature.
![]() These keys are sometimes called “usage” or “special” keys. They may differ in key length and even in the choice of the public-key algorithm. If the PKI requires two key pairs per entity, a user has two certificates:
These keys are sometimes called “usage” or “special” keys. They may differ in key length and even in the choice of the public-key algorithm. If the PKI requires two key pairs per entity, a user has two certificates:
-
 An encryption certificate containing the public key of the user who encrypts the data
An encryption certificate containing the public key of the user who encrypts the data -
 A signature certificate containing the public key of the user who verifies the digital signature of the user
A signature certificate containing the public key of the user who verifies the digital signature of the user
![]() The following scenarios typically use usage keys:
The following scenarios typically use usage keys:
-
 When encryption is used much more frequently than signing, a certain public and private key pair is more exposed due to its frequent usage. In this case, it might be a good idea to shorten its lifetime and change it more often, while having a separate signing private and public key pair with a longer lifetime.
When encryption is used much more frequently than signing, a certain public and private key pair is more exposed due to its frequent usage. In this case, it might be a good idea to shorten its lifetime and change it more often, while having a separate signing private and public key pair with a longer lifetime. -
 When different levels of encryption and digital signing are required, because of legal, export, or performance issues, usage keys allow you to assign different key lengths to the two pairs.
When different levels of encryption and digital signing are required, because of legal, export, or performance issues, usage keys allow you to assign different key lengths to the two pairs. -
 When key recovery is desired (for example, a copy of a user’s private key is kept in a central repository for various backup reasons), usage keys allow you to back up only the private key of the encrypting pair; the signing private key remains with the user, enabling true nonrepudiation.
When key recovery is desired (for example, a copy of a user’s private key is kept in a central repository for various backup reasons), usage keys allow you to back up only the private key of the encrypting pair; the signing private key remains with the user, enabling true nonrepudiation.
![]() The CA, with its private key, is the security-critical component in a PKI system. To make the operation of a CA simpler, and therefore more secure, many key management tasks are often offloaded to registration authorities (RA). RAs are PKI servers that perform management tasks on behalf of the CA, so that the CA can focus on the signing process.
The CA, with its private key, is the security-critical component in a PKI system. To make the operation of a CA simpler, and therefore more secure, many key management tasks are often offloaded to registration authorities (RA). RAs are PKI servers that perform management tasks on behalf of the CA, so that the CA can focus on the signing process.
![]() Usually, the following tasks are offloaded to the RA:
Usually, the following tasks are offloaded to the RA:
-
 Authentication of users when they enroll with the PKI
Authentication of users when they enroll with the PKI -
 Key generation for users who cannot generate their own keys
Key generation for users who cannot generate their own keys -
 Distribution of certificates after enrollment
Distribution of certificates after enrollment
 PKI Standards
PKI Standards
![]() Standardization and interoperability of different PKI vendors is still an issue when interconnecting PKIs. The X.509 standards and the Internet Engineering Task Force (IETF) Public-Key Infrastructure X.509 (PKIX) workgroup have made progress toward publishing a common set of standards for PKI protocols and data formats.
Standardization and interoperability of different PKI vendors is still an issue when interconnecting PKIs. The X.509 standards and the Internet Engineering Task Force (IETF) Public-Key Infrastructure X.509 (PKIX) workgroup have made progress toward publishing a common set of standards for PKI protocols and data formats.
![]() A PKI also uses a number of supporting services, such as Lightweight Directory Access Protocol (LDAP)-accessible X.500 directories.
A PKI also uses a number of supporting services, such as Lightweight Directory Access Protocol (LDAP)-accessible X.500 directories.
![]() Interoperability between a PKI and its supporting services is a concern because many vendors have proposed and implemented proprietary solutions, instead of waiting for standards to develop. The state of interoperability can still be described as basic, even after 10 years of PKI software development.
Interoperability between a PKI and its supporting services is a concern because many vendors have proposed and implemented proprietary solutions, instead of waiting for standards to develop. The state of interoperability can still be described as basic, even after 10 years of PKI software development.
| Note |
|
![]() X.509 is a ubiquitous and well-known standard that defines basic PKI formats, such as certificate and certificate revocation list (CRL) formats, to enable basic interoperability. The standard has been widely used for years with many Internet applications, such as SSL and IPsec.
X.509 is a ubiquitous and well-known standard that defines basic PKI formats, such as certificate and certificate revocation list (CRL) formats, to enable basic interoperability. The standard has been widely used for years with many Internet applications, such as SSL and IPsec.
![]() The X.509 Version 3 (X.509v3) standard defines the format of a digital certificate. This format is already extensively used in the infrastructure of the Internet, in the following ways:
The X.509 Version 3 (X.509v3) standard defines the format of a digital certificate. This format is already extensively used in the infrastructure of the Internet, in the following ways:
-
 Secure web servers use X.509v3 for website authentication in the SSL and TLS protocols.
Secure web servers use X.509v3 for website authentication in the SSL and TLS protocols. -
 Web browsers use X.509v3 for services that implement client certificates in the SSL protocol.
Web browsers use X.509v3 for services that implement client certificates in the SSL protocol. -
 User mail agents that support mail protection using the Secure/Multipurpose Internet Mail Extensions (S/MIME) protocol use X.509.
User mail agents that support mail protection using the Secure/Multipurpose Internet Mail Extensions (S/MIME) protocol use X.509. -
 IPsec VPNs where certificates can be used as a public-key distribution mechanism for IKE RSA-based authentication use X.509.
IPsec VPNs where certificates can be used as a public-key distribution mechanism for IKE RSA-based authentication use X.509.
![]() Certificates are public information. They contain the binding between the names and public keys of entities and are usually published in a centralized directory so that other PKI users can easily access them.
Certificates are public information. They contain the binding between the names and public keys of entities and are usually published in a centralized directory so that other PKI users can easily access them.
![]() In the CA authentication procedure, the first step of the user, when contacting the PKI, is to securely obtain a copy of the public key of the CA. The public key of the CA verifies all the certificates issued by the CA and is vital for the proper operation of the PKI.
In the CA authentication procedure, the first step of the user, when contacting the PKI, is to securely obtain a copy of the public key of the CA. The public key of the CA verifies all the certificates issued by the CA and is vital for the proper operation of the PKI.
![]() The public key of the CA is also distributed in the form of a certificate issued by the CA itself. This certificate is also called a self-signed certificate, because the signer and the holder are the same entity. Only a root CA issues self-signed certificates to itself.
The public key of the CA is also distributed in the form of a certificate issued by the CA itself. This certificate is also called a self-signed certificate, because the signer and the holder are the same entity. Only a root CA issues self-signed certificates to itself.
![]() Public-Key Cryptography Standards (PKCS) provide basic interoperability of applications, which use public-key cryptography. The PKCS define the low-level standardized formats for the secure exchange of arbitrary data, such as a standard format for an encrypted piece of data, a signed piece of data, and so on.
Public-Key Cryptography Standards (PKCS) provide basic interoperability of applications, which use public-key cryptography. The PKCS define the low-level standardized formats for the secure exchange of arbitrary data, such as a standard format for an encrypted piece of data, a signed piece of data, and so on.
![]() The RSA Laboratories website states the following:
The RSA Laboratories website states the following:
![]() The Public-Key Cryptography Standards are specifications produced by RSA Laboratories in cooperation with secure systems developers worldwide for the purpose of accelerating the deployment of public-key cryptography.
The Public-Key Cryptography Standards are specifications produced by RSA Laboratories in cooperation with secure systems developers worldwide for the purpose of accelerating the deployment of public-key cryptography.
![]() There are many defined PKCS standards:
There are many defined PKCS standards:
-
 PKCS #1: RSA Cryptography Standard
PKCS #1: RSA Cryptography Standard -
 PKCS #3: DH Key Agreement Standard
PKCS #3: DH Key Agreement Standard -
 PKCS #5: Password-Based Cryptography Standard
PKCS #5: Password-Based Cryptography Standard -
 PKCS #6: Extended-Certificate Syntax Standard
PKCS #6: Extended-Certificate Syntax Standard -
 PKCS #7: Cryptographic Message Syntax Standard
PKCS #7: Cryptographic Message Syntax Standard -
 PKCS #8: Private-Key Information Syntax Standard
PKCS #8: Private-Key Information Syntax Standard -
 PKCS #10: Certification Request Syntax Standard
PKCS #10: Certification Request Syntax Standard -
 PKCS #12: Personal Information Exchange Syntax Standard
PKCS #12: Personal Information Exchange Syntax Standard -
 PKCS #13: Elliptic Curve Cryptography Standard
PKCS #13: Elliptic Curve Cryptography Standard -
 PKCS #15: Cryptographic Token Information Format Standard
PKCS #15: Cryptographic Token Information Format Standard
| Note |
|
![]() Public-key technology is becoming more widely deployed and is becoming the basis for standards-based security, such as the IPsec and IKE protocols. With the use of public-key certificates in network security protocols comes the need for a certificate management protocol that PKI clients and CA servers can use to support certificate life cycle operations such as certificate enrollment and revocation, and certificate and CRL access. The goal of the Simple Certificate Enrollment Protocol (SCEP) is to support the secure issuance of certificates to network devices in a scalable manner, using existing technology wherever possible.
Public-key technology is becoming more widely deployed and is becoming the basis for standards-based security, such as the IPsec and IKE protocols. With the use of public-key certificates in network security protocols comes the need for a certificate management protocol that PKI clients and CA servers can use to support certificate life cycle operations such as certificate enrollment and revocation, and certificate and CRL access. The goal of the Simple Certificate Enrollment Protocol (SCEP) is to support the secure issuance of certificates to network devices in a scalable manner, using existing technology wherever possible.
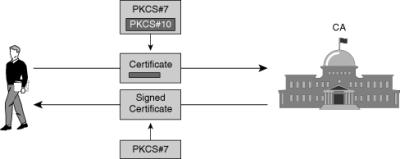
![]() As shown in Figure 4-30, an end entity starts an enrollment transaction by creating a certificate request using PKCS#10 and sends it to the CA or RA that is enveloped using the PKCS#7. After the CA or RA receives the request, it either automatically approves the request or sends the certificate back, or it compels the end entity to wait until the operator can manually authenticate the identity of the requesting end entity.
As shown in Figure 4-30, an end entity starts an enrollment transaction by creating a certificate request using PKCS#10 and sends it to the CA or RA that is enveloped using the PKCS#7. After the CA or RA receives the request, it either automatically approves the request or sends the certificate back, or it compels the end entity to wait until the operator can manually authenticate the identity of the requesting end entity.
 Certificate Authorities
Certificate Authorities
![]() The following features briefly describe CA-based solutions:
The following features briefly describe CA-based solutions:
-
 CAs are the trusted third party in PKI implementations.
CAs are the trusted third party in PKI implementations. -
 The X.509 standard describes an identity and how to store an authentication key. Abstract Syntax Notation One (ASN.1) provides information about the format of the X.509 certificate and the syntax of the fields in the certificate.
The X.509 standard describes an identity and how to store an authentication key. Abstract Syntax Notation One (ASN.1) provides information about the format of the X.509 certificate and the syntax of the fields in the certificate.
![]() Distinguished names (DN) provide a way to identify an entity by using multiple fields to provide hierarchical identification.
Distinguished names (DN) provide a way to identify an entity by using multiple fields to provide hierarchical identification.
| Note |
|
![]() The merging of the X.509 standard with public-key encryption allows the introduction of a trusted third party: the CA. The CA has a pair of asymmetric keys, a private key, and a public key. An X.509 certificate is created to identify the CA. The certificate of the CA contains the following information:
The merging of the X.509 standard with public-key encryption allows the introduction of a trusted third party: the CA. The CA has a pair of asymmetric keys, a private key, and a public key. An X.509 certificate is created to identify the CA. The certificate of the CA contains the following information:
-
 The identity of the CA (for example, a subject containing the identity in the DN format)
The identity of the CA (for example, a subject containing the identity in the DN format) -
 Other parameters (such as serial number, algorithms used, and validity period)
Other parameters (such as serial number, algorithms used, and validity period) -
 The public key of the CA (for example, an RSA public key)
The public key of the CA (for example, an RSA public key) -
 The signature using the private key of the CA (for example, self-signing using the private key of the CA with RSA encryption and the SHA-1 hash algorithm)
The signature using the private key of the CA (for example, self-signing using the private key of the CA with RSA encryption and the SHA-1 hash algorithm)
| Caution |
|
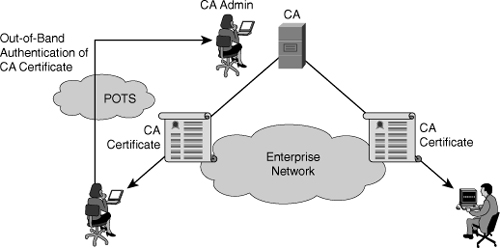
![]() In Figure 4-31, the following steps occur to retrieve the CA certificate:
In Figure 4-31, the following steps occur to retrieve the CA certificate:
|
|
|
|
|
|
|
|
|
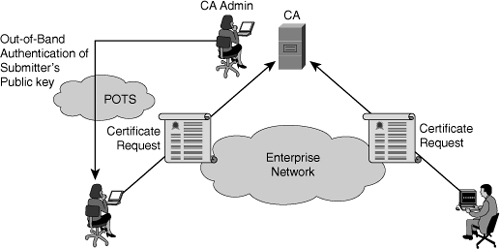
![]() After retrieving the CA certificate, Alice and Bob perform the following steps to submit certificate requests to the CA, as shown in Figure 4-32:
After retrieving the CA certificate, Alice and Bob perform the following steps to submit certificate requests to the CA, as shown in Figure 4-32:
|
|
|
|
|
|
|
|
|
|
|
|
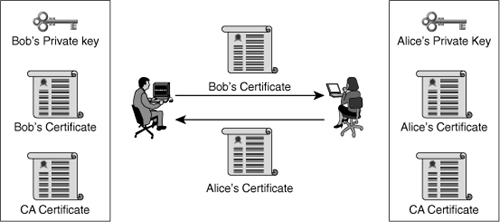
![]() Having installed certificates signed by the same CA, Bob and Alice are now ready to authenticate each other, as shown in Figure 4-33:
Having installed certificates signed by the same CA, Bob and Alice are now ready to authenticate each other, as shown in Figure 4-33:
|
|
|
|
|
|
![]() Compared to other authentication mechanisms, PKI has the following characteristics:
Compared to other authentication mechanisms, PKI has the following characteristics:
-
 To authenticate each other, users have to obtain the certificate of the CA and their own certificate. These steps require the out-of-band verification of the processes. After this verification is complete, the presence of the CA is no longer required until one of the certificates that is involved expires.
To authenticate each other, users have to obtain the certificate of the CA and their own certificate. These steps require the out-of-band verification of the processes. After this verification is complete, the presence of the CA is no longer required until one of the certificates that is involved expires. -
 Public-key systems use asymmetric keys where one is public and the other one is private. One of the features of these algorithms is that whatever is encrypted using one key can only be decrypted using the other key. This provides nonrepudiation.
Public-key systems use asymmetric keys where one is public and the other one is private. One of the features of these algorithms is that whatever is encrypted using one key can only be decrypted using the other key. This provides nonrepudiation. -
 Key management is simplified because two users can freely exchange the certificates. The validity of the received certificates is verified using the public key of the CA, which the users have in their possession.
Key management is simplified because two users can freely exchange the certificates. The validity of the received certificates is verified using the public key of the CA, which the users have in their possession. -
 Because of the strength of the algorithms involved, you can set a very long lifetime for the certificates, typically a lifetime measured in years.
Because of the strength of the algorithms involved, you can set a very long lifetime for the certificates, typically a lifetime measured in years.
![]() The disadvantages of using trusted third parties relate to key management:
The disadvantages of using trusted third parties relate to key management:
-
 A user certificate is compromised (stolen private key): Other users should not accept compromised certificates. The only way to prevent the compromised certificates from being used is to keep a list of all revoked certificates. A server, not necessarily the CA server, must be accessible to users so that they can periodically download the latest CRL and use the list when authenticating other users. If the CRL lists the received certificate of the user, the authentication fails.
A user certificate is compromised (stolen private key): Other users should not accept compromised certificates. The only way to prevent the compromised certificates from being used is to keep a list of all revoked certificates. A server, not necessarily the CA server, must be accessible to users so that they can periodically download the latest CRL and use the list when authenticating other users. If the CRL lists the received certificate of the user, the authentication fails. -
 The certificate of the CA is compromised (stolen private key): This invalidates all certificates signed by the CA. A single CA environment requires the creation of a new CA certificate and the creation of new user certificates. A hierarchical CA environment requires the use of an authority revocation list (ARL), where all child certificates of the compromised CA become invalid if the ARL lists the CA.
The certificate of the CA is compromised (stolen private key): This invalidates all certificates signed by the CA. A single CA environment requires the creation of a new CA certificate and the creation of new user certificates. A hierarchical CA environment requires the use of an authority revocation list (ARL), where all child certificates of the compromised CA become invalid if the ARL lists the CA. -
 The CA administrator: The human factor is an additional limitation of the CA-based solution. To lessen the impact, the CA administrator should follow strict rules when issuing certificates to users. A security policy should define the steps required to create certificates (for example, mandatory out-of-band verification of all initial enrollment procedures or verification steps for CA administrators before approving a certificate requests).
The CA administrator: The human factor is an additional limitation of the CA-based solution. To lessen the impact, the CA administrator should follow strict rules when issuing certificates to users. A security policy should define the steps required to create certificates (for example, mandatory out-of-band verification of all initial enrollment procedures or verification steps for CA administrators before approving a certificate requests).
| Note |
|
![]() When you use certificates in IP networks, you might need to combine public-key authentication with another authentication mechanism to increase the level of security and provide more authorization options. For example, IPsec using certificates for authentication and Extended Authentication (XAUTH) with one-time password hardware tokens would be a superior authentication scheme when compared to certificates alone.
When you use certificates in IP networks, you might need to combine public-key authentication with another authentication mechanism to increase the level of security and provide more authorization options. For example, IPsec using certificates for authentication and Extended Authentication (XAUTH) with one-time password hardware tokens would be a superior authentication scheme when compared to certificates alone.
![]() Certificates were traditionally used at the application layer to provide strong authentication for applications; however, nowadays implementations can vary as to which layer on which they operate. Each application may have a different implementation of the actual authentication process, but they all use a similar type of certificate in the X.509 format.
Certificates were traditionally used at the application layer to provide strong authentication for applications; however, nowadays implementations can vary as to which layer on which they operate. Each application may have a different implementation of the actual authentication process, but they all use a similar type of certificate in the X.509 format.
![]() SSL, which operates at the session layer of the OSI model, is probably the most widely used certificate-based authentication. SSL includes the negotiation of keys that are used to encrypt the SSL session. Many applications use SSL to provide authentication and encryption; the most widely used application is HTTPS. Other well-known applications that were using poor authentication and no encryption were modified to use SSL, such as Simple Mail Transfer Protocol (SMTP), LDAP, and Post Office Protocol Version 3 (POP3).
SSL, which operates at the session layer of the OSI model, is probably the most widely used certificate-based authentication. SSL includes the negotiation of keys that are used to encrypt the SSL session. Many applications use SSL to provide authentication and encryption; the most widely used application is HTTPS. Other well-known applications that were using poor authentication and no encryption were modified to use SSL, such as Simple Mail Transfer Protocol (SMTP), LDAP, and Post Office Protocol Version 3 (POP3).
![]() Email has experienced many extensions. One of the important extensions was the introduction of Multipurpose Internet Mail Extension (MIME), which allowed arbitrary data to be included in an email. Another extension was to provide security to entire mail messages or parts of mail messages. Secure/MIME (S/MIME) authenticates and encrypts email messages.
Email has experienced many extensions. One of the important extensions was the introduction of Multipurpose Internet Mail Extension (MIME), which allowed arbitrary data to be included in an email. Another extension was to provide security to entire mail messages or parts of mail messages. Secure/MIME (S/MIME) authenticates and encrypts email messages.
![]() Pretty Good Privacy (PGP) is an application that was originally developed by Phil Zimmerman, a privacy advocate, so that end users could engage in confidential communications using encryption. The most frequent use of PGP has been to secure email.
Pretty Good Privacy (PGP) is an application that was originally developed by Phil Zimmerman, a privacy advocate, so that end users could engage in confidential communications using encryption. The most frequent use of PGP has been to secure email.
![]() Certificates are also used at the network layer, or at the application layer, by network devices. Cisco routers, Cisco VPN concentrators, and Cisco PIX firewalls can use certificates to authenticate IPsec peers.
Certificates are also used at the network layer, or at the application layer, by network devices. Cisco routers, Cisco VPN concentrators, and Cisco PIX firewalls can use certificates to authenticate IPsec peers.
![]() Cisco switches can use certificates to authenticate end devices connecting to LAN ports. Authentication uses 802.1X between the adjacent devices. The authentication can be proxied to a central access control server (ACS) via the Extensible Authentication Protocol with TLS (EAP-TLS).
Cisco switches can use certificates to authenticate end devices connecting to LAN ports. Authentication uses 802.1X between the adjacent devices. The authentication can be proxied to a central access control server (ACS) via the Extensible Authentication Protocol with TLS (EAP-TLS).
![]() Cisco routers can also provide Telnet 3270 support that does not include encryption or strong authentication. Cisco routers can now use SSL to establish secure TN3270 sessions.
Cisco routers can also provide Telnet 3270 support that does not include encryption or strong authentication. Cisco routers can now use SSL to establish secure TN3270 sessions.
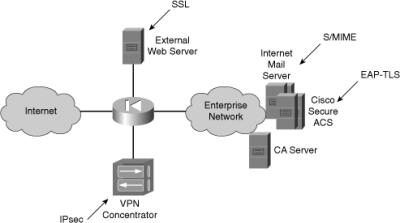
![]() Figure 4-34 illustrates a network where certificates are used for various purposes. A single CA server can facilitate many applications that require digital certificates for authentication purposes.
Figure 4-34 illustrates a network where certificates are used for various purposes. A single CA server can facilitate many applications that require digital certificates for authentication purposes.
![]() Using CA servers is therefore a solution that simplifies the management of authentication and provides strong security due to the strength of cryptographic mechanisms used in combination with digital certificates.
Using CA servers is therefore a solution that simplifies the management of authentication and provides strong security due to the strength of cryptographic mechanisms used in combination with digital certificates.
Summary
![]() The key points covered in this chapter are as follows:
The key points covered in this chapter are as follows:
-
 A cryptosystem is made up of a combination of hashing, symmetric, and asymmetric algorithms.
A cryptosystem is made up of a combination of hashing, symmetric, and asymmetric algorithms. -
 Symmetric algorithms use a single key for encrypting and decrypting. Generally speaking, symmetric algorithms are the strongest and fastest algorithms and therefore are used for most encryption.
Symmetric algorithms use a single key for encrypting and decrypting. Generally speaking, symmetric algorithms are the strongest and fastest algorithms and therefore are used for most encryption. -
 Hashing algorithms use a one-way process designed to provide integrity. Usually, successful decryption of a digest provides proof of integrity and authenticity.
Hashing algorithms use a one-way process designed to provide integrity. Usually, successful decryption of a digest provides proof of integrity and authenticity. -
 Asymmetric algorithms use a key pair for the encrypting/decrypting process. One key encrypts, and the other member of the pair decrypts.
Asymmetric algorithms use a key pair for the encrypting/decrypting process. One key encrypts, and the other member of the pair decrypts.
 References
References
![]() For additional information, refer to these resources:
For additional information, refer to these resources:
-
 Kahn, D. The Codebreakers (Scribner, 1996)
Kahn, D. The Codebreakers (Scribner, 1996) -
 Singh, S. The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography (Knopf Publishing Group, 1999)
Singh, S. The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography (Knopf Publishing Group, 1999) -
 U.S. Department of Commerce, http://www.commerce.gov
U.S. Department of Commerce, http://www.commerce.gov -
 Kaliski, B. TWIRL and RSA Key Size, http://www.rsasecurity.com/rsalabs/node.asp?id=2004
Kaliski, B. TWIRL and RSA Key Size, http://www.rsasecurity.com/rsalabs/node.asp?id=2004 -
 Giry, D. Cryptographic Key Length Recommendation, http://www.keylength.com/en/3/
Giry, D. Cryptographic Key Length Recommendation, http://www.keylength.com/en/3/ -
 NIST. AES, http://www.nist.gov/aes
NIST. AES, http://www.nist.gov/aes -
 RSA Laboratories. RSA Laboratories’ Frequently Asked Questions About Today’s Cryptography, Version 4.1 (RSA Security Inc., 2000)
RSA Laboratories. RSA Laboratories’ Frequently Asked Questions About Today’s Cryptography, Version 4.1 (RSA Security Inc., 2000) -
 Federal Information Processing Standards Publications. FIPS PUB 180-1, http://www.itl.nist.gov/fipspubs/fip180-1.htm
Federal Information Processing Standards Publications. FIPS PUB 180-1, http://www.itl.nist.gov/fipspubs/fip180-1.htm -
 IETF. Public-Key Infrastructure (X.509) (pkix), http://www.ietf.org/html.charters/pkix-charter.html
IETF. Public-Key Infrastructure (X.509) (pkix), http://www.ietf.org/html.charters/pkix-charter.html -
 RSA Laboratories. Crypto FAQ, http://www.rsa.com/rsalabs/node.asp?id=2152
RSA Laboratories. Crypto FAQ, http://www.rsa.com/rsalabs/node.asp?id=2152 -
 RSA Laboratories. Public-Key Cryptography Standards (PKCS), http://www.rsa.com/rsalabs/node.asp?id=2124
RSA Laboratories. Public-Key Cryptography Standards (PKCS), http://www.rsa.com/rsalabs/node.asp?id=2124


2 comments
Perfect ! This article truly explains all about cryptography. All the key points and even basics are covered in this article. I am highly pleased with it. Thank you so much for sharing.
digital signature software
Great Blog I Have Read Your Blog It Is Very Useful For Me Thank you for posting and sharing such great information.can you help me in finding out more detail on Fundamentals of Cryptography.
Post a Comment