Examining Symmetric Encryption
![]() Modern encryption algorithms rely on encryption keys to provide confidentiality of encrypted data. With symmetric encryption algorithms, the same key is used to encrypt and decrypt data. The sections that follow describe the principles behind symmetric encryption, provide examples of major symmetric encryption algorithms, and examine their operations, strengths, and weaknesses.
Modern encryption algorithms rely on encryption keys to provide confidentiality of encrypted data. With symmetric encryption algorithms, the same key is used to encrypt and decrypt data. The sections that follow describe the principles behind symmetric encryption, provide examples of major symmetric encryption algorithms, and examine their operations, strengths, and weaknesses.
 Symmetric Encryption Overview
Symmetric Encryption Overview
![]() Symmetric encryption algorithms are the most commonly used form of cryptography. Because of the simplicity of their mathematics, they are extremely fast when compared to asymmetric algorithms. Also, because symmetric encryption algorithms are stronger, they can use shorter key lengths, which help increase their speed of execution in software.
Symmetric encryption algorithms are the most commonly used form of cryptography. Because of the simplicity of their mathematics, they are extremely fast when compared to asymmetric algorithms. Also, because symmetric encryption algorithms are stronger, they can use shorter key lengths, which help increase their speed of execution in software.
![]() Some of the characteristics of symmetric algorithms are as follows:
Some of the characteristics of symmetric algorithms are as follows:
-
 Faster than asymmetric algorithms.
Faster than asymmetric algorithms. -
 Much shorter key lengths than asymmetric algorithms.
Much shorter key lengths than asymmetric algorithms. -
 Simpler mathematics than asymmetric algorithms.
Simpler mathematics than asymmetric algorithms. -
 One key is used for both encryption and decryption.
One key is used for both encryption and decryption. -
 Sometimes referred to as private-key encryption.
Sometimes referred to as private-key encryption.
![]() DES, 3DES, AES, Blowfish, RC2/4/6, and SEAL are common symmetric algorithms. Most of the encryption done worldwide today uses symmetric algorithms.
DES, 3DES, AES, Blowfish, RC2/4/6, and SEAL are common symmetric algorithms. Most of the encryption done worldwide today uses symmetric algorithms.
![]() Earlier, Figure 4-10 provided graphical representation of a symmetrical key.
Earlier, Figure 4-10 provided graphical representation of a symmetrical key.
![]() Modern symmetric algorithms use key lengths that range from 40 to 256 bits. This range gives symmetric algorithms keyspaces that range from 240 (1,099,511,627,776 possible keys) to 2256 (1.5 * 1077) possible keys. This large range is the difference between whether or not the algorithm is vulnerable to a brute-force attack. If you use a key length of 40 bits, your encryption is likely to be broken easily using a brute-force attack. In contrast, if your key length is 256 bits, it is unlikely that a brute-force attack will be successful, because the key space is too large.
Modern symmetric algorithms use key lengths that range from 40 to 256 bits. This range gives symmetric algorithms keyspaces that range from 240 (1,099,511,627,776 possible keys) to 2256 (1.5 * 1077) possible keys. This large range is the difference between whether or not the algorithm is vulnerable to a brute-force attack. If you use a key length of 40 bits, your encryption is likely to be broken easily using a brute-force attack. In contrast, if your key length is 256 bits, it is unlikely that a brute-force attack will be successful, because the key space is too large.
![]() On average, a brute-force attack will succeed halfway through the keyspace. Key lengths that are too short can have the entire possible keyspace stored in RAM on a server cluster of a cracker, which makes it possible for the algorithm to be cracked in real time.
On average, a brute-force attack will succeed halfway through the keyspace. Key lengths that are too short can have the entire possible keyspace stored in RAM on a server cluster of a cracker, which makes it possible for the algorithm to be cracked in real time.
![]() Assuming that the algorithms are mathematically and cryptographically sound, Table 4-1 illustrates ongoing expectations for valid key lengths. What is also assumed in such calculations is that computing power will continue to grow at its present rate and the ability to perform brute-force attacks will grow at the same rate.
Assuming that the algorithms are mathematically and cryptographically sound, Table 4-1 illustrates ongoing expectations for valid key lengths. What is also assumed in such calculations is that computing power will continue to grow at its present rate and the ability to perform brute-force attacks will grow at the same rate.
|
|
|
|
| |
|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Caution |
|
| Note |
|
 DES: Features and Functions
DES: Features and Functions
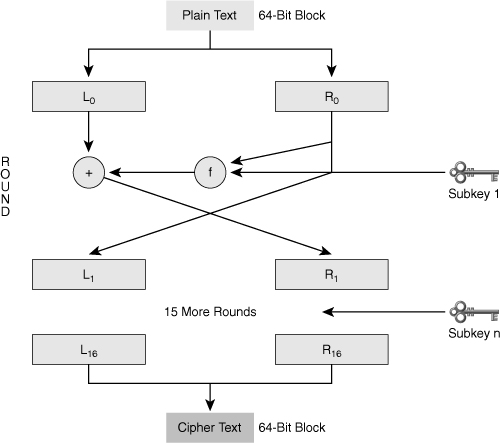
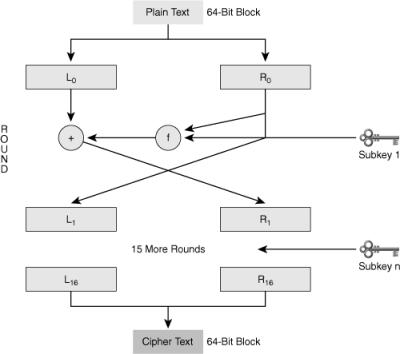
![]() Data Encryption Standard (DES) is a symmetric encryption algorithm that usually operates in block mode, in which it encrypts data in 64-bit blocks. The DES algorithm is essentially a sequence of permutations and substitutions of data bits, combined with the encryption key. The same algorithm and key are used for both encryption and decryption. Cryptography researchers have scrutinized DES for nearly 35 years and have found no significant flaws.
Data Encryption Standard (DES) is a symmetric encryption algorithm that usually operates in block mode, in which it encrypts data in 64-bit blocks. The DES algorithm is essentially a sequence of permutations and substitutions of data bits, combined with the encryption key. The same algorithm and key are used for both encryption and decryption. Cryptography researchers have scrutinized DES for nearly 35 years and have found no significant flaws.
![]() Because DES is based on simple mathematical functions, it can easily be implemented and accelerated in hardware.
Because DES is based on simple mathematical functions, it can easily be implemented and accelerated in hardware.
![]() DES has a fixed key length. The key is actually 64 bits long but only 56 bits are used for encryption, the remaining 8 bits are used for parity; the least significant bit of each key byte is used to indicate odd parity.
DES has a fixed key length. The key is actually 64 bits long but only 56 bits are used for encryption, the remaining 8 bits are used for parity; the least significant bit of each key byte is used to indicate odd parity.
![]() A DES key is always 56 bits long. When you use DES with a weaker encryption of a 40-bit key, it actually means that the encryption key is 40 secret bits and 16 known bits, which make the key length 56 bits. In this case, DES actually has a key strength of 40 bits.
A DES key is always 56 bits long. When you use DES with a weaker encryption of a 40-bit key, it actually means that the encryption key is 40 secret bits and 16 known bits, which make the key length 56 bits. In this case, DES actually has a key strength of 40 bits.
DES Modes of Operation
![]() To encrypt or decrypt more than 64 bits of data, DES uses two different types of ciphers:
To encrypt or decrypt more than 64 bits of data, DES uses two different types of ciphers:
-
 Block ciphers: Operate on fixed-length groups of bits, termed blocks, with an unvarying transformation
Block ciphers: Operate on fixed-length groups of bits, termed blocks, with an unvarying transformation -
 Stream ciphers: Operate on individual digits one at a time with the transformation varying during the encryption
Stream ciphers: Operate on individual digits one at a time with the transformation varying during the encryption
![]() DES uses two standardized block cipher modes:
DES uses two standardized block cipher modes:
-
 Electronic Code Book (ECB)
Electronic Code Book (ECB) -
 Cipher Block Chaining (CBC)
Cipher Block Chaining (CBC)
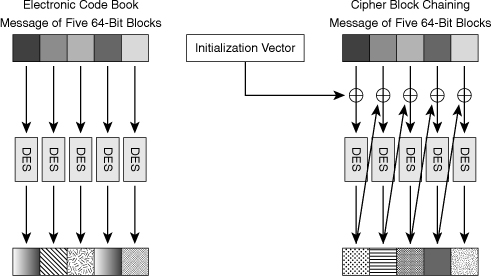
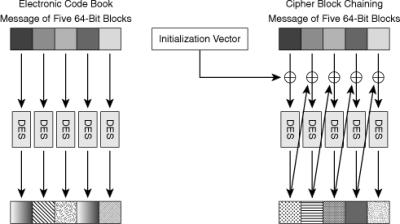
![]() Figure 4-14 illustrates the differences between ECB mode and CBC mode.
Figure 4-14 illustrates the differences between ECB mode and CBC mode.
![]() ECB mode serially encrypts each 64-bit plaintext block using the same 56-bit key. If two identical plaintext blocks are encrypted using the same key, their ciphertext blocks are the same. Therefore, an attacker could identify similar or identical traffic flowing through a communications channel, and use this information. The attacker could then build a catalogue of messages, which have a certain meaning, and replay them later, without knowing their real meaning. For example, an attacker might capture a login sequence of someone with administrative privilege whose traffic is protected by DES-ECB and then replay it. That risk is undesirable so CBC mode was invented to mitigate this risk.
ECB mode serially encrypts each 64-bit plaintext block using the same 56-bit key. If two identical plaintext blocks are encrypted using the same key, their ciphertext blocks are the same. Therefore, an attacker could identify similar or identical traffic flowing through a communications channel, and use this information. The attacker could then build a catalogue of messages, which have a certain meaning, and replay them later, without knowing their real meaning. For example, an attacker might capture a login sequence of someone with administrative privilege whose traffic is protected by DES-ECB and then replay it. That risk is undesirable so CBC mode was invented to mitigate this risk.
![]() In CBC mode, shown in Figure 4-15, each 64-bit plaintext block is exclusive ORed (XORed) bitwise with the previous ciphertext block and then is encrypted using the DES key. Because of this process, the encryption of each block depends on previous blocks. Encryption of the same 64-bit plaintext block can result in different ciphertext blocks. CBC mode can help guard against certain attacks, but it cannot help against sophisticated cryptanalysis or an extended brute-force attack.
In CBC mode, shown in Figure 4-15, each 64-bit plaintext block is exclusive ORed (XORed) bitwise with the previous ciphertext block and then is encrypted using the DES key. Because of this process, the encryption of each block depends on previous blocks. Encryption of the same 64-bit plaintext block can result in different ciphertext blocks. CBC mode can help guard against certain attacks, but it cannot help against sophisticated cryptanalysis or an extended brute-force attack.
![]() In CBC mode, each 64-bit plaintext block is XORed bitwise with the previous ciphertext block and then is encrypted with the DES key. Therefore, the encryption of each block depends on previous blocks, and because the key changes each time, the same 64-bit plaintext block can encrypt to different ciphertext blocks. The first block is XORed with an initialization vector, which is a public, random value prepended to each message to bootstrap the chaining process.
In CBC mode, each 64-bit plaintext block is XORed bitwise with the previous ciphertext block and then is encrypted with the DES key. Therefore, the encryption of each block depends on previous blocks, and because the key changes each time, the same 64-bit plaintext block can encrypt to different ciphertext blocks. The first block is XORed with an initialization vector, which is a public, random value prepended to each message to bootstrap the chaining process.
| Note |
|
![]() In stream cipher mode, the cipher uses previous ciphertext and the secret key to generate a pseudorandom stream of bits, which only the secret key can generate. To encrypt data, the data is XORed with the pseudorandom stream bit by bit, or sometimes byte by byte, to obtain the ciphertext. The decryption procedure is the same: The receiver generates the same random stream using the secret key, and XORs the ciphertext with the pseudorandom stream to obtain the plaintext.
In stream cipher mode, the cipher uses previous ciphertext and the secret key to generate a pseudorandom stream of bits, which only the secret key can generate. To encrypt data, the data is XORed with the pseudorandom stream bit by bit, or sometimes byte by byte, to obtain the ciphertext. The decryption procedure is the same: The receiver generates the same random stream using the secret key, and XORs the ciphertext with the pseudorandom stream to obtain the plaintext.
![]() To encrypt or decrypt more than 64 bits of data, DES uses two common stream cipher modes:
To encrypt or decrypt more than 64 bits of data, DES uses two common stream cipher modes:
-
 Cipher Feedback (CFB): CFB is similar to CBC and can encrypt any number of bits, including single bits or single characters.
Cipher Feedback (CFB): CFB is similar to CBC and can encrypt any number of bits, including single bits or single characters. -
 Output Feedback (OFB): OFB generates keystream blocks, which are then XORed with the plaintext blocks to get the ciphertext.
Output Feedback (OFB): OFB generates keystream blocks, which are then XORed with the plaintext blocks to get the ciphertext.
DES Security Guidelines
![]() You should consider doing several things to protect the security of DES-encrypted data:
You should consider doing several things to protect the security of DES-encrypted data:
-
 Change keys frequently to help prevent brute-force attacks.
Change keys frequently to help prevent brute-force attacks. -
 Use a secure channel to communicate the DES key from the sender to the receiver.
Use a secure channel to communicate the DES key from the sender to the receiver. -
 Consider using DES in CBC mode. With CBC, the encryption of each 64-bit block depends on previous blocks. CBC is the most widely used mode of DES.
Consider using DES in CBC mode. With CBC, the encryption of each 64-bit block depends on previous blocks. CBC is the most widely used mode of DES. -
 Verify that a key is not part of the weak or semi-weak key list before using it. DES has 4 weak keys and 12 semi-weak keys. Because there are 256 possible DES keys, the chance of picking one of these keys is small. However, because testing the key has no significant impact on the encryption time, it is recommended that you test the key. The keys that should be avoided are listed in Section 3.6 of Publication 74 of the Federal Information Processing Standards, http://www.itl.nist.gov/fipspubs/fip74.htm.
Verify that a key is not part of the weak or semi-weak key list before using it. DES has 4 weak keys and 12 semi-weak keys. Because there are 256 possible DES keys, the chance of picking one of these keys is small. However, because testing the key has no significant impact on the encryption time, it is recommended that you test the key. The keys that should be avoided are listed in Section 3.6 of Publication 74 of the Federal Information Processing Standards, http://www.itl.nist.gov/fipspubs/fip74.htm.
| Note |
|
 3DES: Features and Functions
3DES: Features and Functions
![]() With advances in computer processing power, the original 56-bit DES key became too short to withstand even medium-budget attackers. One way to increase the DES effective key length, without changing the well-analyzed algorithm itself, is to use the same algorithm with different keys several times in a row.
With advances in computer processing power, the original 56-bit DES key became too short to withstand even medium-budget attackers. One way to increase the DES effective key length, without changing the well-analyzed algorithm itself, is to use the same algorithm with different keys several times in a row.
![]() The technique of applying DES three times in a row to a plaintext block is called 3DES. Brute-force attacks on 3DES are considered unfeasible today, and because the basic algorithm has been well tested in the field for more than 35 years, it is considered very trustworthy.
The technique of applying DES three times in a row to a plaintext block is called 3DES. Brute-force attacks on 3DES are considered unfeasible today, and because the basic algorithm has been well tested in the field for more than 35 years, it is considered very trustworthy.
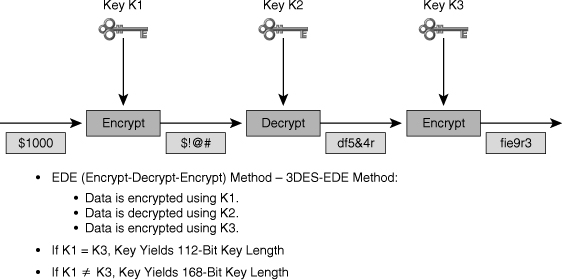
![]() 3DES uses a method called 3DES-Encrypt-Decrypt-Encrypt (3DES-EDE) to encrypt plaintext. 3DES-EDE includes the following steps:
3DES uses a method called 3DES-Encrypt-Decrypt-Encrypt (3DES-EDE) to encrypt plaintext. 3DES-EDE includes the following steps:
|
|
|
|
|
|
|
|
|
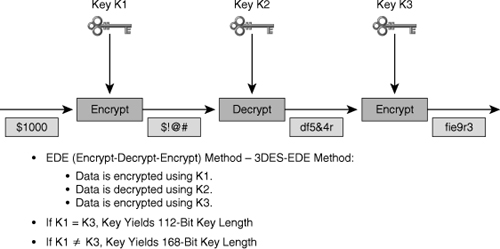
![]() The 3DES-EDE procedure, shown in Figure 4-16, provides encryption with an effective key length of 168 bits. If keys K1 and K3 are equal, as in some implementations, a less-secure encryption of 112 bits is achieved.
The 3DES-EDE procedure, shown in Figure 4-16, provides encryption with an effective key length of 168 bits. If keys K1 and K3 are equal, as in some implementations, a less-secure encryption of 112 bits is achieved.
![]() The following procedure is used to decrypt a 3DES-EDE block:
The following procedure is used to decrypt a 3DES-EDE block:
|
|
|
|
|
|
|
|
|
| Note |
|
 AES: Features and Functions
AES: Features and Functions
![]() For a number of years, it was recognized that DES would eventually reach the end of its usefulness. In 1997, the AES initiative was announced, and the public was invited to propose candidate encryption schemes, one of which could be chosen as the encryption standard to replace DES. There were rigorous reviews of 15 original candidates. Rijndael, Twofish, and RC6 were among the finalists. Rijndael was ultimately selected.
For a number of years, it was recognized that DES would eventually reach the end of its usefulness. In 1997, the AES initiative was announced, and the public was invited to propose candidate encryption schemes, one of which could be chosen as the encryption standard to replace DES. There were rigorous reviews of 15 original candidates. Rijndael, Twofish, and RC6 were among the finalists. Rijndael was ultimately selected.
The Rijndael Cipher
![]() On October 2, 2000, the U.S. National Institute of Standards and Technology (NIST) announced the selection of the Rijndael cipher as the AES algorithm. The Rijndael cipher, developed by Joan Daemen and Vincent Rijmen, has a variable block length and key length. The algorithm currently specifies how to use keys with a length of 128, 192, or 256 bits to encrypt blocks with a length of 128, 192, or 256 bits, which provides nine different combinations of key length and block length. Both block length and key length can be extended very easily in multiples of 32 bits.
On October 2, 2000, the U.S. National Institute of Standards and Technology (NIST) announced the selection of the Rijndael cipher as the AES algorithm. The Rijndael cipher, developed by Joan Daemen and Vincent Rijmen, has a variable block length and key length. The algorithm currently specifies how to use keys with a length of 128, 192, or 256 bits to encrypt blocks with a length of 128, 192, or 256 bits, which provides nine different combinations of key length and block length. Both block length and key length can be extended very easily in multiples of 32 bits.
![]() The U.S. Secretary of Commerce approved the adoption of AES as an official U.S. government standard, effective May 26, 2002. AES is listed in Annex A of FIPS Publication 140-2 as an approved security function.
The U.S. Secretary of Commerce approved the adoption of AES as an official U.S. government standard, effective May 26, 2002. AES is listed in Annex A of FIPS Publication 140-2 as an approved security function.
| Note |
|
![]() Rijndael is an iterated block cipher, which means that the initial input block and cipher key undergo multiple transformation cycles before producing output. The algorithm can operate over a variable-length block using variable-length keys; a 128-, 192-, or 256-bit key can be used to encrypt data blocks that are 128, 192, or 256 bits long, and all nine combinations of key and block length are possible. The accepted AES implementation of Rijndael contains only some of the capabilities of the Rijndael algorithm. The algorithm is written so that the block length or the key length or both can easily be extended in multiples of 32 bits, and the system is specifically designed for efficient implementation in hardware or software on a range of processors.
Rijndael is an iterated block cipher, which means that the initial input block and cipher key undergo multiple transformation cycles before producing output. The algorithm can operate over a variable-length block using variable-length keys; a 128-, 192-, or 256-bit key can be used to encrypt data blocks that are 128, 192, or 256 bits long, and all nine combinations of key and block length are possible. The accepted AES implementation of Rijndael contains only some of the capabilities of the Rijndael algorithm. The algorithm is written so that the block length or the key length or both can easily be extended in multiples of 32 bits, and the system is specifically designed for efficient implementation in hardware or software on a range of processors.
AES Versus 3DES
![]() AES was chosen to replace DES and 3DES, because the key length of AES makes it stronger than DES and AES runs faster than 3DES on comparable hardware. AES is more efficient than DES and 3DES on comparable hardware, usually by a factor of five when it is compared with DES. Also, AES is more suitable for high-throughput, low-latency environments, especially if pure software encryption is used. However, AES is a relatively young algorithm, and, as the golden rule of cryptography states, a more mature algorithm is always more trusted. 3DES is therefore a more conservative and more trusted choice in terms of strength, because it has been analyzed for around 35 years.
AES was chosen to replace DES and 3DES, because the key length of AES makes it stronger than DES and AES runs faster than 3DES on comparable hardware. AES is more efficient than DES and 3DES on comparable hardware, usually by a factor of five when it is compared with DES. Also, AES is more suitable for high-throughput, low-latency environments, especially if pure software encryption is used. However, AES is a relatively young algorithm, and, as the golden rule of cryptography states, a more mature algorithm is always more trusted. 3DES is therefore a more conservative and more trusted choice in terms of strength, because it has been analyzed for around 35 years.
AES Availability in the Cisco Product Line
![]() AES is available in the following Cisco VPN devices as an encryption transform, applied to IPsec-protected traffic:
AES is available in the following Cisco VPN devices as an encryption transform, applied to IPsec-protected traffic:
-
 Cisco IOS Release 12.2(13)T and later
Cisco IOS Release 12.2(13)T and later -
 Cisco PIX Firewall Software Version 6.3 and later
Cisco PIX Firewall Software Version 6.3 and later -
 Cisco ASA Software Version 7.0 and later
Cisco ASA Software Version 7.0 and later -
 Cisco VPN 3000 Software Version 3.6 and later
Cisco VPN 3000 Software Version 3.6 and later
| Note |
|
 SEAL: Features and Functions
SEAL: Features and Functions
![]() The Software Encryption Algorithm (SEAL) is an alternative algorithm to software-based DES, 3DES, and AES. SEAL encryption uses a 160-bit encryption key and has a lower impact on the CPU compared to other software-based algorithms. The SEAL encryption feature provides support for the SEAL algorithm in Cisco IOS IPsec implementations. SEAL support was added to Cisco IOS Software Release 12.3(7)T.
The Software Encryption Algorithm (SEAL) is an alternative algorithm to software-based DES, 3DES, and AES. SEAL encryption uses a 160-bit encryption key and has a lower impact on the CPU compared to other software-based algorithms. The SEAL encryption feature provides support for the SEAL algorithm in Cisco IOS IPsec implementations. SEAL support was added to Cisco IOS Software Release 12.3(7)T.
| Note |
|
![]() Several restrictions apply to SEAL:
Several restrictions apply to SEAL:
-
 Your Cisco router and the other peer must support IPsec.
Your Cisco router and the other peer must support IPsec. -
 Your Cisco router and the other peer must support the k9 subsystem of the IOS (k9 subsystem refers to long keys). An example would be IOS c2600-ipbasek9-mz.124-17b.bin, which is the IP Base Security 12.4(17b) IOS for Cisco 2600.
Your Cisco router and the other peer must support the k9 subsystem of the IOS (k9 subsystem refers to long keys). An example would be IOS c2600-ipbasek9-mz.124-17b.bin, which is the IP Base Security 12.4(17b) IOS for Cisco 2600. -
 This feature is available only on Cisco equipment.
This feature is available only on Cisco equipment.
| Caution |
|
 Rivest Ciphers: Features and Functions
Rivest Ciphers: Features and Functions
![]() The RC family of algorithms is widely deployed in many networking applications because of their favorable speed and variable key length capabilities.
The RC family of algorithms is widely deployed in many networking applications because of their favorable speed and variable key length capabilities.
![]() The RC algorithms were designed all or in part by Ronald Rivest. Some of the most widely used RC algorithms are as follows:
The RC algorithms were designed all or in part by Ronald Rivest. Some of the most widely used RC algorithms are as follows:
-
 RC2: This algorithm is a variable key-size block cipher that was designed as a “drop-in” replacement for DES.
RC2: This algorithm is a variable key-size block cipher that was designed as a “drop-in” replacement for DES. -
 RC4: This algorithm is a variable key-size Vernam stream cipher often used in file encryption products and for secure communications, such as within SSL. It is not considered a one-time pad because its key is not random. The cipher can be expected to run very quickly in software and is considered secure, although it can be implemented insecurely, as in Wired Equivalent Privacy (WEP).
RC4: This algorithm is a variable key-size Vernam stream cipher often used in file encryption products and for secure communications, such as within SSL. It is not considered a one-time pad because its key is not random. The cipher can be expected to run very quickly in software and is considered secure, although it can be implemented insecurely, as in Wired Equivalent Privacy (WEP). -
 RC5: This algorithm is a fast block cipher that has variable block size and variable key size. With a 64-bit block size, RC5 can be used as a drop-in replacement for DES.
RC5: This algorithm is a fast block cipher that has variable block size and variable key size. With a 64-bit block size, RC5 can be used as a drop-in replacement for DES. -
 RC6: This algorithm is a block cipher that was designed by Rivest, Sidney, and Yin and is based on RC5. Its main design goal was to meet the requirement of AES.
RC6: This algorithm is a block cipher that was designed by Rivest, Sidney, and Yin and is based on RC5. Its main design goal was to meet the requirement of AES.
Examining Cryptographic Hashes and Digital Signatures
![]() Cryptographic hashes and digital signatures play an important part in modern cryptosystems. Hashes and digital signatures provide verification and authentication and play an important role in nonrepudiation. It is important to understand the basic mechanisms of these algorithms and some of the issues involved in choosing a particular hashing algorithm or digital signature method.
Cryptographic hashes and digital signatures play an important part in modern cryptosystems. Hashes and digital signatures provide verification and authentication and play an important role in nonrepudiation. It is important to understand the basic mechanisms of these algorithms and some of the issues involved in choosing a particular hashing algorithm or digital signature method.
 Overview of Hash Algorithms
Overview of Hash Algorithms
![]() Hashing is a mechanism that provides data-integrity assurance. Hashing is based on a one-way mathematical function: functions that are relatively easy to compute, but significantly harder to reverse, as explained earlier in this chapter using the coffee-grinding analogy.
Hashing is a mechanism that provides data-integrity assurance. Hashing is based on a one-way mathematical function: functions that are relatively easy to compute, but significantly harder to reverse, as explained earlier in this chapter using the coffee-grinding analogy.
![]() The hashing process uses a hash function, which is a one-way function of input data that produces a fixed-length digest of output data, also known as a fingerprint. The digest is cryptographically very strong; it is impossible to recover input data from its digest. If the input data changes just a little bit, the digest changes substantially. This is known as the avalanche effect. Essentially, the fingerprint that results from hashing data uniquely identifies that data. If you are given only a fingerprint, it is computationally unfeasible to generate data that would result in that fingerprint.
The hashing process uses a hash function, which is a one-way function of input data that produces a fixed-length digest of output data, also known as a fingerprint. The digest is cryptographically very strong; it is impossible to recover input data from its digest. If the input data changes just a little bit, the digest changes substantially. This is known as the avalanche effect. Essentially, the fingerprint that results from hashing data uniquely identifies that data. If you are given only a fingerprint, it is computationally unfeasible to generate data that would result in that fingerprint.
![]() Hashing is often applied in the following situations:
Hashing is often applied in the following situations:
-
 To generate one-time and one-way responses to challenges in authentication protocols such as PPP Challenge Handshake Authentication Protocol (CHAP), Microsoft NT Domain, and Extensible Authentication Protocol-Message Digest 5 (EAP-MD5)
To generate one-time and one-way responses to challenges in authentication protocols such as PPP Challenge Handshake Authentication Protocol (CHAP), Microsoft NT Domain, and Extensible Authentication Protocol-Message Digest 5 (EAP-MD5) -
 To provide proof of the integrity of data, such as that provided with file integrity checkers, digitally signed contracts, and Public Key Infrastructure (PKI) certificates
To provide proof of the integrity of data, such as that provided with file integrity checkers, digitally signed contracts, and Public Key Infrastructure (PKI) certificates -
 To provide proof of authenticity when it is used with a symmetric secret authentication key, such as IPsec or routing protocol authentication
To provide proof of authenticity when it is used with a symmetric secret authentication key, such as IPsec or routing protocol authentication
| Key Topic |
|
![]() A hash function, (H), is a transformation that takes an input (x), and returns a fixed-size string, which is called the hash value h. The formula for the calculation is h = H(x).
A hash function, (H), is a transformation that takes an input (x), and returns a fixed-size string, which is called the hash value h. The formula for the calculation is h = H(x).
![]() A cryptographic hash function should have the following general properties:
A cryptographic hash function should have the following general properties:
-
 The input can be any length.
The input can be any length. -
 The output has a fixed length.
The output has a fixed length. -
 H(x) is relatively easy to compute for any given x.
H(x) is relatively easy to compute for any given x. -
 H(x) is one way and not reversible.
H(x) is one way and not reversible. -
 H(x) is collision free.
H(x) is collision free.
![]() If a hash function is hard to invert, it is considered a one-way hash. Hard to invert means that given a hash value h, it is computationally infeasible to find some input, (x), such that H(x) = h. H is said to be a weakly collision-free hash function if given a message x, it is computationally infeasible to find a message y not equal to x such that H(x) = H(y). A strongly collision-free hash function H is one for which it is computationally infeasible to find any two messages x and y such that H(x) = H(y).
If a hash function is hard to invert, it is considered a one-way hash. Hard to invert means that given a hash value h, it is computationally infeasible to find some input, (x), such that H(x) = h. H is said to be a weakly collision-free hash function if given a message x, it is computationally infeasible to find a message y not equal to x such that H(x) = H(y). A strongly collision-free hash function H is one for which it is computationally infeasible to find any two messages x and y such that H(x) = H(y).
![]() Figure 4-12, shown earlier in this chapter, illustrates the hashing process. Data of arbitrary length is input into the hash function, and the result of the hash function is the fixed-length digest or fingerprint. Hashing is similar to the calculation of CRC checksums, but is cryptographically stronger. That is, given a CRC value, it is easy to generate data with the same CRC. However, with hash functions, it is computationally infeasible for an attacker, given a hash value h, to find some input, (x), such that H(x) = h.
Figure 4-12, shown earlier in this chapter, illustrates the hashing process. Data of arbitrary length is input into the hash function, and the result of the hash function is the fixed-length digest or fingerprint. Hashing is similar to the calculation of CRC checksums, but is cryptographically stronger. That is, given a CRC value, it is easy to generate data with the same CRC. However, with hash functions, it is computationally infeasible for an attacker, given a hash value h, to find some input, (x), such that H(x) = h.
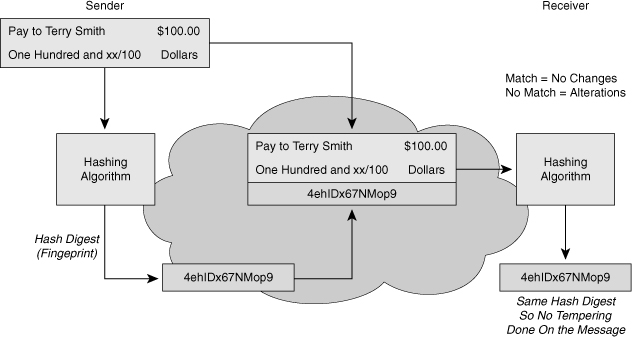
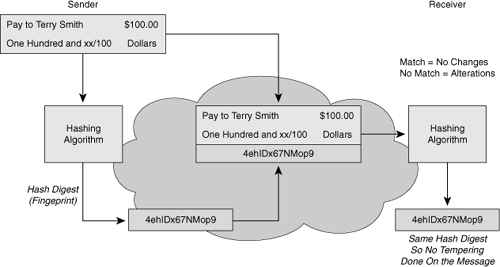
![]() Figure 4-17 illustrates hashing in action. The sender wants to ensure that the message is not altered on its way to the receiver. The sending device inputs the message into a hashing algorithm and computes its fixed-length digest or fingerprint. This fingerprint is then attached to the message, the message and the hash are in plaintext, and sent to the receiver. The receiving device removes the fingerprint from the message and inputs the message into the same hashing algorithm. If the hash that is computed by the receiving device is equal to the one that is attached to the message, the message has not been altered during transit.
Figure 4-17 illustrates hashing in action. The sender wants to ensure that the message is not altered on its way to the receiver. The sending device inputs the message into a hashing algorithm and computes its fixed-length digest or fingerprint. This fingerprint is then attached to the message, the message and the hash are in plaintext, and sent to the receiver. The receiving device removes the fingerprint from the message and inputs the message into the same hashing algorithm. If the hash that is computed by the receiving device is equal to the one that is attached to the message, the message has not been altered during transit.
![]() Hashing does not add security to the message. When the message traverses the network, a potential attacker could intercept the message, change it, recalculate the hash, and append it to the message. Hashing only prevents the message from being changed accidentally, such as by a communication error. There is nothing unique to the sender in the hashing procedure; therefore, anyone can compute a hash for any data, as long as they have the correct hash function.
Hashing does not add security to the message. When the message traverses the network, a potential attacker could intercept the message, change it, recalculate the hash, and append it to the message. Hashing only prevents the message from being changed accidentally, such as by a communication error. There is nothing unique to the sender in the hashing procedure; therefore, anyone can compute a hash for any data, as long as they have the correct hash function.
![]() Thus, hash functions are helpful to ensure that data did not change accidentally, but it cannot ensure that data was not deliberately changed.
Thus, hash functions are helpful to ensure that data did not change accidentally, but it cannot ensure that data was not deliberately changed.
![]() These are two well-known hash functions:
These are two well-known hash functions:
-
 Message Digest 5 (MD5) with 128-bit digests
Message Digest 5 (MD5) with 128-bit digests -
 Secure Hash Algorithm 1 (SHA-1) with 160-bit digests
Secure Hash Algorithm 1 (SHA-1) with 160-bit digests
 Overview of Hashed Message Authentication Codes
Overview of Hashed Message Authentication Codes
![]() Hash functions are the basis of the protection mechanism of Hashed Message Authentication Codes (HMAC). HMACs use existing hash functions, but with a significant difference; HMACs add a secret key as input to the hash function. Only the sender and the receiver know the secret key, and the output of the hash function now depends on the input data and the secret key. Therefore, only parties who have access to that secret key can compute the digest of an HMAC function. This behavior defeats man-in-the-middle attacks and provides authentication of the data origin. If two parties share a secret key and use HMAC functions for authentication, a properly constructed HMAC digest of a message that a party has received indicates that the other party was the originator of the message, because it is the only other entity possessing the secret key.
Hash functions are the basis of the protection mechanism of Hashed Message Authentication Codes (HMAC). HMACs use existing hash functions, but with a significant difference; HMACs add a secret key as input to the hash function. Only the sender and the receiver know the secret key, and the output of the hash function now depends on the input data and the secret key. Therefore, only parties who have access to that secret key can compute the digest of an HMAC function. This behavior defeats man-in-the-middle attacks and provides authentication of the data origin. If two parties share a secret key and use HMAC functions for authentication, a properly constructed HMAC digest of a message that a party has received indicates that the other party was the originator of the message, because it is the only other entity possessing the secret key.
![]() Cisco technologies use two well-known HMAC functions:
Cisco technologies use two well-known HMAC functions:
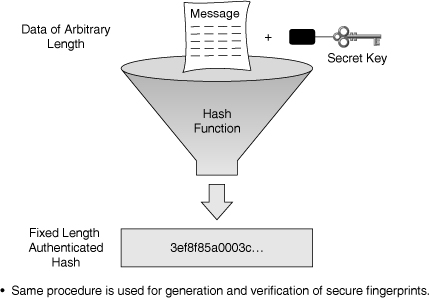
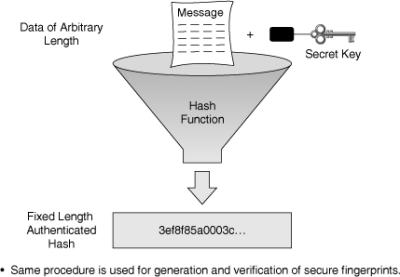
![]() Figure 4-18 illustrates how an HMAC digest is created. Data of an arbitrary length is input into the hash function, together with a secret key. The result is the fixed-length hash that depends on the data and the secret key.
Figure 4-18 illustrates how an HMAC digest is created. Data of an arbitrary length is input into the hash function, together with a secret key. The result is the fixed-length hash that depends on the data and the secret key.
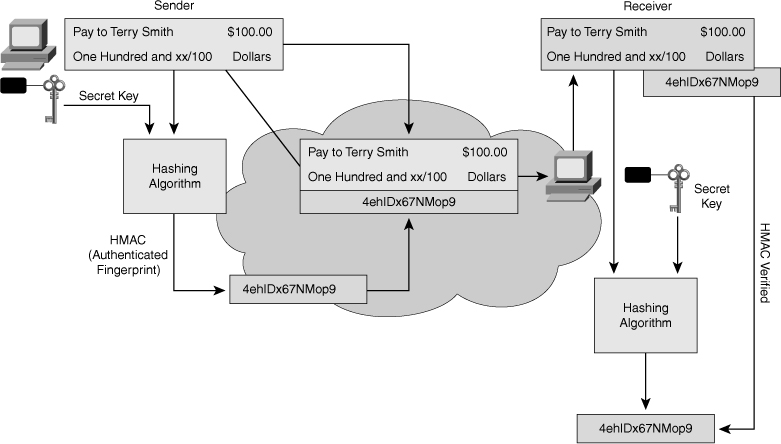
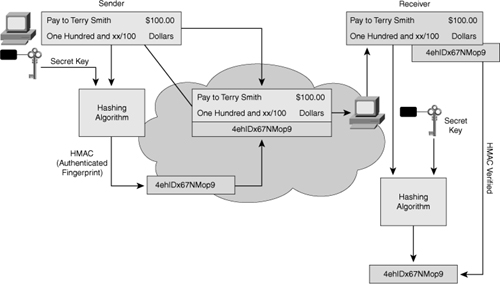
![]() Figure 4-19 illustrates HMAC in action. The sender wants to ensure that the message is not altered in transit, and wants to provide a way for the receiver to authenticate the origin of the message.
Figure 4-19 illustrates HMAC in action. The sender wants to ensure that the message is not altered in transit, and wants to provide a way for the receiver to authenticate the origin of the message.
![]() The sending device inputs data and the secret key into the hashing algorithm and calculates the fixed-length HMAC digest or fingerprint. This authenticated fingerprint is then attached to the message and sent to the receiver. The receiving device removes the fingerprint from the message and uses the plaintext message with the secret key as input to the same hashing function. If the fingerprint calculated by the receiving device is equal to the fingerprint that was sent, the message has not been altered. In addition, the origin of the message is authenticated, because only the sender possesses a copy of the shared secret key. The HMAC function has ensured the authenticity of the message.
The sending device inputs data and the secret key into the hashing algorithm and calculates the fixed-length HMAC digest or fingerprint. This authenticated fingerprint is then attached to the message and sent to the receiver. The receiving device removes the fingerprint from the message and uses the plaintext message with the secret key as input to the same hashing function. If the fingerprint calculated by the receiving device is equal to the fingerprint that was sent, the message has not been altered. In addition, the origin of the message is authenticated, because only the sender possesses a copy of the shared secret key. The HMAC function has ensured the authenticity of the message.
| Note |
|
![]() Cisco products use hashing for entity-authentication, data-integrity, and data-authenticity purposes:
Cisco products use hashing for entity-authentication, data-integrity, and data-authenticity purposes:
-
 IPsec gateways and clients use hashing algorithms, such as MD5 and SHA-1 in HMAC mode, to provide packet integrity and authenticity.
IPsec gateways and clients use hashing algorithms, such as MD5 and SHA-1 in HMAC mode, to provide packet integrity and authenticity. -
 Cisco IOS routers use hashing with secret keys in an HMAC-like manner, to add authentication information to routing protocol updates.
Cisco IOS routers use hashing with secret keys in an HMAC-like manner, to add authentication information to routing protocol updates. -
 Cisco software images that you can download from Cisco.com have an MD5-based checksum available so that customers can check the integrity of downloaded images.
Cisco software images that you can download from Cisco.com have an MD5-based checksum available so that customers can check the integrity of downloaded images. -
 Hashing can also be used in a feedback-like mode to encrypt data; for example, TACACS+ uses MD5 to encrypt its session.
Hashing can also be used in a feedback-like mode to encrypt data; for example, TACACS+ uses MD5 to encrypt its session.
 MD5: Features and Functions
MD5: Features and Functions
![]() The MD5 algorithm is a ubiquitous hashing algorithm that was developed by Ron Rivest and is used in a variety of Internet applications today. Hashing was illustrated previously in Figure 4-12.
The MD5 algorithm is a ubiquitous hashing algorithm that was developed by Ron Rivest and is used in a variety of Internet applications today. Hashing was illustrated previously in Figure 4-12.
![]() MD5 is a one-way function that makes it easy to compute a hash from the given input data, but makes it unfeasible to compute input data given only a hash. MD5 is also collision resistant, which means that two messages with the same hash are very unlikely to occur. MD5 is essentially a complex sequence of simple binary operations, such as exclusive OR (XORs) and rotations, that are performed on input data and produce a 128-bit digest.
MD5 is a one-way function that makes it easy to compute a hash from the given input data, but makes it unfeasible to compute input data given only a hash. MD5 is also collision resistant, which means that two messages with the same hash are very unlikely to occur. MD5 is essentially a complex sequence of simple binary operations, such as exclusive OR (XORs) and rotations, that are performed on input data and produce a 128-bit digest.
![]() The main algorithm itself is based on a compression function, which operates on blocks. The input is a data block plus a feedback of previous blocks. 512-bit blocks are divided into 16, 32-bit sub-blocks. These blocks are then rearranged with simple operations in a main loop, which consists of four rounds. The output of the algorithm is a set of four, 32-bit blocks, which concatenate to form a single 128-bit hash value. The message length is also encoded into the digest.
The main algorithm itself is based on a compression function, which operates on blocks. The input is a data block plus a feedback of previous blocks. 512-bit blocks are divided into 16, 32-bit sub-blocks. These blocks are then rearranged with simple operations in a main loop, which consists of four rounds. The output of the algorithm is a set of four, 32-bit blocks, which concatenate to form a single 128-bit hash value. The message length is also encoded into the digest.
![]() MD5 is based on MD4, an earlier algorithm. MD4 has been broken, and currently MD5 is considered less secure than SHA-1 by many authorities on cryptography, such as the ICSA Labs (http://www.icsalabs.com). These authorities consider MD5 less secure than SHA-1 because some noncritical weaknesses have been found in one of the MD5 building blocks, causing uneasy feelings inside the cryptographic community. The availability of the SHA-1 and RACE Integrity Primitives Evaluation Message Digest (RIPEMD)-160 HMAC functions, which do not show such weaknesses and use a stronger (160-bit) digest, makes MD5 a second choice as far as hash methods are concerned.
MD5 is based on MD4, an earlier algorithm. MD4 has been broken, and currently MD5 is considered less secure than SHA-1 by many authorities on cryptography, such as the ICSA Labs (http://www.icsalabs.com). These authorities consider MD5 less secure than SHA-1 because some noncritical weaknesses have been found in one of the MD5 building blocks, causing uneasy feelings inside the cryptographic community. The availability of the SHA-1 and RACE Integrity Primitives Evaluation Message Digest (RIPEMD)-160 HMAC functions, which do not show such weaknesses and use a stronger (160-bit) digest, makes MD5 a second choice as far as hash methods are concerned.
 SHA-1: Features and Functions
SHA-1: Features and Functions
![]() The U.S. National Institute of Standards and Technology (NIST) developed the Secure Hash Algorithm (SHA), the algorithm that is specified in the Secure Hash Standard (SHS). SHA-1 is a revision to the SHA that was published in 1994; the revision corrected an unpublished flaw in SHA. Its design is similar to the MD4 family of hash functions that Ron Rivest developed.
The U.S. National Institute of Standards and Technology (NIST) developed the Secure Hash Algorithm (SHA), the algorithm that is specified in the Secure Hash Standard (SHS). SHA-1 is a revision to the SHA that was published in 1994; the revision corrected an unpublished flaw in SHA. Its design is similar to the MD4 family of hash functions that Ron Rivest developed.
![]() The SHA-1 algorithm takes a message of less than 264 bits in length and produces a 160-bit message digest. The algorithm is slightly slower than MD5, but the larger message digest makes it more secure against brute-force collision and inversion attacks.
The SHA-1 algorithm takes a message of less than 264 bits in length and produces a 160-bit message digest. The algorithm is slightly slower than MD5, but the larger message digest makes it more secure against brute-force collision and inversion attacks.
![]() You can find the official standard text at http://www.itl.nist.gov/fipspubs/fip180-1.htm.
You can find the official standard text at http://www.itl.nist.gov/fipspubs/fip180-1.htm.
| Note |
|
![]() Because both MD5 and SHA-1 are based on MD4, MD5 and SHA-1 are very similar. SHA-1 should be more resistant to brute-force attacks because its digest is 32 bits longer than the MD5 digest.
Because both MD5 and SHA-1 are based on MD4, MD5 and SHA-1 are very similar. SHA-1 should be more resistant to brute-force attacks because its digest is 32 bits longer than the MD5 digest.
![]() SHA-1 involves 80 steps, and MD5 involves 64 steps. The SHA-1 algorithm must also process a 160-bit buffer rather than the 128-bit buffer of MD5. Therefore, it is expected that MD5 would execute more quickly, given the same device.
SHA-1 involves 80 steps, and MD5 involves 64 steps. The SHA-1 algorithm must also process a 160-bit buffer rather than the 128-bit buffer of MD5. Therefore, it is expected that MD5 would execute more quickly, given the same device.
![]() In general, when given a choice, SHA-1 is the preferred hashing algorithm. MD5 is arguably less trusted today, and for most commercial environments, such risks should be avoided.
In general, when given a choice, SHA-1 is the preferred hashing algorithm. MD5 is arguably less trusted today, and for most commercial environments, such risks should be avoided.
![]() When choosing a hashing algorithm, SHA-1 is generally preferred over MD5. MD5 has not been proven to contain any critical flaws, but its security is questionable today. You might consider MD5 if performance is an issue, because using MD5 might increase performance slightly, but not substantially. However, the risk exists that it might be discovered to be substantially weaker than SHA-1.
When choosing a hashing algorithm, SHA-1 is generally preferred over MD5. MD5 has not been proven to contain any critical flaws, but its security is questionable today. You might consider MD5 if performance is an issue, because using MD5 might increase performance slightly, but not substantially. However, the risk exists that it might be discovered to be substantially weaker than SHA-1.
![]() With HMACs, you must take care to distribute secret keys only to the parties that are involved, because compromise of the secret key enables any other party to forge and change packets, violating data integrity.
With HMACs, you must take care to distribute secret keys only to the parties that are involved, because compromise of the secret key enables any other party to forge and change packets, violating data integrity.
 Overview of Digital Signatures
Overview of Digital Signatures
![]() When data is exchanged over untrusted networks, several major security issues must be determined:
When data is exchanged over untrusted networks, several major security issues must be determined:
-
 Has data changed in transit: Hashing and HMAC functions rely on a cumbersome exchange of secret keys between parties to provide the guarantee of integrity.
Has data changed in transit: Hashing and HMAC functions rely on a cumbersome exchange of secret keys between parties to provide the guarantee of integrity. -
 Whether a document is authentic: Hashing and HMAC can provide some guarantee of authenticity, but only by using secret keys between two parties. Hashing and HMAC cannot guarantee authenticity of a transaction or a document to a third party.
Whether a document is authentic: Hashing and HMAC can provide some guarantee of authenticity, but only by using secret keys between two parties. Hashing and HMAC cannot guarantee authenticity of a transaction or a document to a third party.
![]() Digital signatures are often used in the following situations:
Digital signatures are often used in the following situations:
-
 To provide a unique proof of data source, which can be generated only by a single party, such as with contract signing in e-commerce environments
To provide a unique proof of data source, which can be generated only by a single party, such as with contract signing in e-commerce environments -
 To authenticate a user by using the private key of that user, and the signature it generates
To authenticate a user by using the private key of that user, and the signature it generates -
 To prove the authenticity and integrity of PKI certificates
To prove the authenticity and integrity of PKI certificates -
 To provide a secure time stamp, such as with a central trusted time source
To provide a secure time stamp, such as with a central trusted time source
![]() Suppose a customer sends transaction instructions via an email to a stockbroker, and the transaction turns out badly for the customer. It is conceivable that the customer could claim never to have sent the transaction order, or that someone forged the email. The brokerage could protect itself by requiring the use of digital signatures before accepting instructions via email.
Suppose a customer sends transaction instructions via an email to a stockbroker, and the transaction turns out badly for the customer. It is conceivable that the customer could claim never to have sent the transaction order, or that someone forged the email. The brokerage could protect itself by requiring the use of digital signatures before accepting instructions via email.
![]() Handwritten signatures have long been used as a proof of authorship of, or at least agreement with, the contents of a document. Digital signatures can provide the same functionality as handwritten signatures, and much more.
Handwritten signatures have long been used as a proof of authorship of, or at least agreement with, the contents of a document. Digital signatures can provide the same functionality as handwritten signatures, and much more.
![]() Digital signatures provide three basic security services in secure communications:
Digital signatures provide three basic security services in secure communications:
-
 Authenticity of digitally signed data: Digital signatures authenticate a source, proving that a certain party has seen and has signed the data in question.
Authenticity of digitally signed data: Digital signatures authenticate a source, proving that a certain party has seen and has signed the data in question. -
 Integrity of digitally signed data: Digital signatures guarantee that the data has not changed from the time it was signed.
Integrity of digitally signed data: Digital signatures guarantee that the data has not changed from the time it was signed. -
 Nonrepudiation of the transaction: The recipient can take the data to a third party, which accepts the digital signature as a proof that this data exchange did take place. The signing party cannot repudiate that it has signed the data.
Nonrepudiation of the transaction: The recipient can take the data to a third party, which accepts the digital signature as a proof that this data exchange did take place. The signing party cannot repudiate that it has signed the data.
| Note |
|
![]() To achieve the preceding goals, digital signatures have the following properties:
To achieve the preceding goals, digital signatures have the following properties:
-
 The signature is authentic: The signature convinces the recipient of the document that the signer signed the document.
The signature is authentic: The signature convinces the recipient of the document that the signer signed the document. -
 The signature is not forgeable: The signature is proof that the signer, and no one else, signed the document.
The signature is not forgeable: The signature is proof that the signer, and no one else, signed the document. -
 The signature is not reusable: The signature is a part of the document and cannot be moved to a different document.
The signature is not reusable: The signature is a part of the document and cannot be moved to a different document. -
 The signature is unalterable: After a document is signed, the document cannot be altered without detection.
The signature is unalterable: After a document is signed, the document cannot be altered without detection. -
 The signature cannot be repudiated: The signature and the document are physical things. The signer cannot claim later that they did not sign it.
The signature cannot be repudiated: The signature and the document are physical things. The signer cannot claim later that they did not sign it.
![]() Well-known asymmetric algorithms, such as Rivest, Shamir, and Adleman (RSA) or Digital Signature Algorithm (DSA), are typically used to perform digital signing.
Well-known asymmetric algorithms, such as Rivest, Shamir, and Adleman (RSA) or Digital Signature Algorithm (DSA), are typically used to perform digital signing.
![]() In some countries, including the United States, digital signatures are considered equivalent to handwritten signatures, if they meet certain provisions. Some of these provisions include the proper protection of the certificate authority, the trusted signer of all other public keys, and the proper protection of the private keys of the users. In such a scenario, users are responsible for keeping their private keys private, because a stolen private key can be used to “steal” their identity.
In some countries, including the United States, digital signatures are considered equivalent to handwritten signatures, if they meet certain provisions. Some of these provisions include the proper protection of the certificate authority, the trusted signer of all other public keys, and the proper protection of the private keys of the users. In such a scenario, users are responsible for keeping their private keys private, because a stolen private key can be used to “steal” their identity.
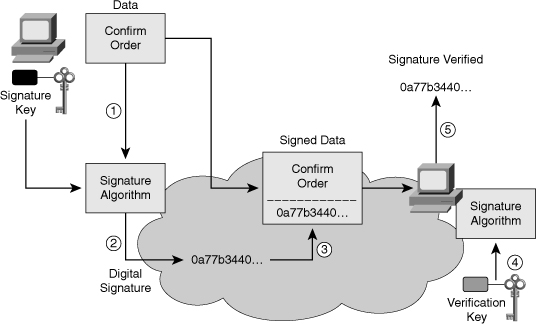
![]() Later in this chapter you will have the opportunity to delve deeper in the mechanic of digital signatures, but for now Figure 4-20 illustrates the basic functioning of digital signatures:
Later in this chapter you will have the opportunity to delve deeper in the mechanic of digital signatures, but for now Figure 4-20 illustrates the basic functioning of digital signatures:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Key Topic |
|
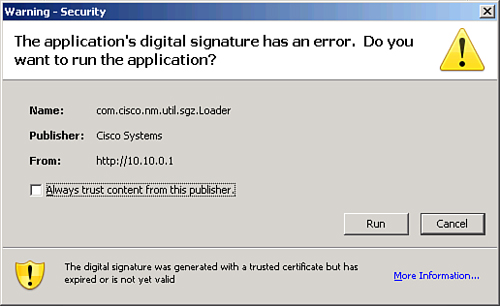
![]() Digital signatures are commonly used to provide assurance of the code authenticity and integrity of both mobile and classic software. In the case of Figure 4-21, the user is being warned that the digital certificate has expired or is no longer valid. The executable files, or possibly the whole installation package of a program, are wrapped with a digitally signed envelope, which allows the end user to verify the signature before installing the software.
Digital signatures are commonly used to provide assurance of the code authenticity and integrity of both mobile and classic software. In the case of Figure 4-21, the user is being warned that the digital certificate has expired or is no longer valid. The executable files, or possibly the whole installation package of a program, are wrapped with a digitally signed envelope, which allows the end user to verify the signature before installing the software.
![]() Digitally signing code provides several assurances about the code:
Digitally signing code provides several assurances about the code:
-
 The code has not been modified since it has left the software publisher.
The code has not been modified since it has left the software publisher. -
 The code is authentic and is actually sourced by the publisher.
The code is authentic and is actually sourced by the publisher. -
 The publisher undeniably publishes the code. This provides nonrepudiation of the act of publishing.
The publisher undeniably publishes the code. This provides nonrepudiation of the act of publishing.
![]() The digital signature could be forged only if someone obtained the private key of the publisher. The assurance level of digital signatures is extremely high if the private key is protected properly.
The digital signature could be forged only if someone obtained the private key of the publisher. The assurance level of digital signatures is extremely high if the private key is protected properly.
![]() The user of the software must also obtain the public key, which is used to verify the signature. The user can obtain the key in a secure fashion; for example, the key could be included with the installation of the operating system, or transferred securely over the network (for example, using the PKI and certificate authorities).
The user of the software must also obtain the public key, which is used to verify the signature. The user can obtain the key in a secure fashion; for example, the key could be included with the installation of the operating system, or transferred securely over the network (for example, using the PKI and certificate authorities).
 DSS: Features and Functions
DSS: Features and Functions
![]() In 1994, NIST selected the DSA as the Digital Signature Standard (DSS). DSA is based on the discrete logarithm problem and can only provide digital signatures.
In 1994, NIST selected the DSA as the Digital Signature Standard (DSS). DSA is based on the discrete logarithm problem and can only provide digital signatures.
![]() DSA signature generation is faster than signature verification; however, with the RSA algorithm, signature verification is much faster than signature generation.
DSA signature generation is faster than signature verification; however, with the RSA algorithm, signature verification is much faster than signature generation.
![]() There have been several criticisms of DSA:
There have been several criticisms of DSA:
-
 DSA lacks the flexibility of RSA.
DSA lacks the flexibility of RSA. -
 The verification of signatures is too slow.
The verification of signatures is too slow. -
 The process by which NIST chose DSA was too secretive and arbitrary.
The process by which NIST chose DSA was too secretive and arbitrary.
![]() In response to these criticisms, the DSS now incorporates two additional algorithm choices:
In response to these criticisms, the DSS now incorporates two additional algorithm choices:
-
 Digital Signature Using Reversible Public Key Cryptography, which uses RSA
Digital Signature Using Reversible Public Key Cryptography, which uses RSA -
 Elliptic Curve Digital Signature Algorithm (ECDSA)
Elliptic Curve Digital Signature Algorithm (ECDSA)
![]() Protection of the private key is of the highest importance when using digital signatures. If the signature key of an entity is compromised, the attacker can sign data in the name of that entity, and repudiation is not possible. To exchange verification keys in a scalable fashion, you must deploy a PKI in most scenarios.
Protection of the private key is of the highest importance when using digital signatures. If the signature key of an entity is compromised, the attacker can sign data in the name of that entity, and repudiation is not possible. To exchange verification keys in a scalable fashion, you must deploy a PKI in most scenarios.
![]() You also need to decide whether RSA or DSA is more appropriate for the situation:
You also need to decide whether RSA or DSA is more appropriate for the situation:
-
 DSA signature generation is faster than signature verification.
DSA signature generation is faster than signature verification. -
 RSA signature verification is much faster than signature generation.
RSA signature verification is much faster than signature generation.
![]() Cisco products use digital signatures for entity-authentication, data-integrity, and data-authenticity purposes:
Cisco products use digital signatures for entity-authentication, data-integrity, and data-authenticity purposes:
-
 IPsec gateways and clients use digital signatures to authenticate their Internet Key Exchange (IKE) sessions, if you choose digital certificates and the IKE RSA signature authentication method.
IPsec gateways and clients use digital signatures to authenticate their Internet Key Exchange (IKE) sessions, if you choose digital certificates and the IKE RSA signature authentication method. -
 Cisco SSL endpoints, such as Cisco IOS HTTP servers, and the Cisco Adaptive Security Device Manager (ASDM), use digital signatures to prove the identity of the SSL server.
Cisco SSL endpoints, such as Cisco IOS HTTP servers, and the Cisco Adaptive Security Device Manager (ASDM), use digital signatures to prove the identity of the SSL server. -
 Some of the service-provider-oriented voice management protocols, for billing and settlement, use digital signatures to authenticate the involved parties.
Some of the service-provider-oriented voice management protocols, for billing and settlement, use digital signatures to authenticate the involved parties.

1 comments
Thanks for posting the fundamentals of cryptography on your blog. I have read both the article and found this information simply amazing. You have explained the complete concept of cryptography in detail.
electronic signature in word
Post a Comment